Решение: Обозначим расстояние от пункта А в пункт Б за S (км), тогда скорость плота равна: S/6 км/час, равная скорости течения реки. Обозначим скорость лодки за (х) км/час, тогда лодка проплыла из пункта Б в пункт А против течения реки, согласно условия задачи, за 6 часов или: S/(x-S/6)=6 S=6x-(6S/6) 6S=36x-6S 6S+6S=36x 12S=36x х=12S : 36 х=S/3 - скорость лодки Из пункта А в пункт Б лодка проплывёт по течению со скоростью: S/3+S/6=(2S+S)/6=3S/6=S/2 Время потраченное на этот путь из пункта А в пункт Б составит: S : S/2=S*2/S=2 (часа)
-
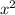+ 8х + 3х - 24 = -х (х - 3) + 8 (х - 3) = (х - 3) (8 - х)
-
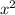- 11х + 2х + 22 = -х (х + 11) + 2 (х + 11) = (х + 11) (2 - х)
-
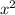- 17х + 3х + 51 = -х (х + 17) + 3 (х + 17) = (х + 17) (3 - х)
-2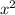
- 22х + 11х + 121 = -2х (х + 11) + 11 (х + 11) = (х + 11) (11 - 2х)
-4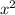
+ 10х - 12х +30 = -4х (х + 3) + 10 (х + 3) = (х + 3) (10 - 4х)
-5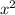
- 10х + 4х + 8 = -5х (х + 2) + 4 (х + 2) = (х + 2) (4 - 5х)
4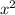
+ 16х - 5х - 20 = 4х (х + 4) - 5 (х + 4) = (х + 4) (4х - 5)
9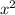
- 27х + 6х + 18 = 9х (х - 3) + 6 (х + 3)
В последнем, скорее всего, какая-то ошибка, потому что преобразовать его в произведение невозможно.
Обозначим расстояние от пункта А в пункт Б за S (км), тогда скорость плота равна: S/6 км/час, равная скорости течения реки.
Обозначим скорость лодки за (х) км/час, тогда лодка проплыла из пункта Б в пункт А против течения реки, согласно условия задачи, за 6 часов или:
S/(x-S/6)=6
S=6x-(6S/6)
6S=36x-6S
6S+6S=36x
12S=36x
х=12S : 36
х=S/3 - скорость лодки
Из пункта А в пункт Б лодка проплывёт по течению со скоростью:
S/3+S/6=(2S+S)/6=3S/6=S/2
Время потраченное на этот путь из пункта А в пункт Б составит:
S : S/2=S*2/S=2 (часа)
ответ: за 2 часа