Если коротко, контроша, 8 класс, .

1.посчитайте сумму выражения.

а) 9^(4) : 27 (-3)

б) 2 × 1,4^(-2) - 7 (-2)

2. данное выражение и посчитайте его сумму, если a=0,125; b=8
0,2a^(-2)b (4)-5a (3)b (-3)

3.решите

{2х/3+y/6=12

{3x/5-y/4=6

5. a)5a-5/6-3 × 86-24/a^(2)-1

б) 5x-10y/x^(2)-9y^(2) : x-2y/x^(2)-6xy+9^(2)

7.сократите дробь

x^(3) - 8/x^(2)+2x+4

8. выражение

(1/a^(2)+ab + 1/ab+b^(2)) : 1/ab

Показать ответ

Ответ:

диментор

13.07.2022 08:17

Объяснение:

1. a - ширина прямоугольника, см.

Площадь прямоугольника: S=ab.

21=a(a+7)

a²+7a-21=0; D=49+84=133

a₁=(-7-√133)/2 - так как a₁<0, то этот корень не подходит по смыслу к данной задаче.

a₂=(-7+√133)/2 см - ширина прямоугольника.

b₂=(-7+√133)/2 +7=(-7+14+√133)/2=(7+√133)/2 см - длина прямоугольника.

Периметр прямоугольника:

P=2(a+b)=2((-7+√133)/2 +(7+√133)/2)=2√133 см

x - скорость байдарки, км/ч.

8/(x-3) +10/(x+3)=3

8(x+3)+10(x-3)=3(x-3)(x+3)

8x+24+10x-30=3(x²-9)

3x²-27-18x+6=0

3x²-18x-21=0 |3

x²-6x-7=0

x₁+x₂=6; 7-1=6

x₁x₂=-7; 7·(-1)=-7

x₁=7 км/ч - скорость байдарки.

x₂=-1 - этот корень не подходит по смыслу к данной задаче.

7-3=4 км/ч - скорость байдарки против течения.

0,0(0 оценок)

Ответ:

chorna202

12.03.2022 04:29

Вероятностью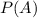 P(A) события 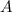при проведении некоторого испытания называют отношение числа тех исходов 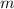, в результате которых наступает событие 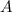, к общему числу 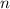всех (равновозможных между собой) исходов этого испытания.

$P(A) = \dfrac{m}{n}$

Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти.

Пусть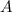 - событие, состоящее в том, что из урны, где находится 25 желтых, 15 синих, 10 красных шаров, можно наудачу взять три красных шара.

Из 10 красных шаров нужно выбрать 3 (порядок не имеет значения) - это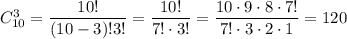 $C^{3}_{10} = \dfrac{10!}{(10-3)!3!} = \dfrac{10!}{7!\cdot 3!}= \dfrac{10 \cdot 9 \cdot 8 \cdot 7!}{7! \cdot 3 \cdot 2 \cdot 1} = 120$

Выбрать 3 шара из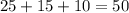 25 + 15 + 10 = 50 (порядок не имеет значения) можно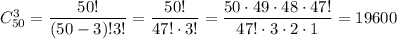 $C^{3}_{50} = \dfrac{50!}{(50-3)!3!}=\dfrac{50!}{47! \cdot 3!} =\dfrac{50 \cdot 49 \cdot 48 \cdot 47!}{47! \cdot 3 \cdot 2 \cdot 1} =19600$

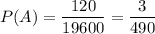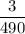Следовательно, согласно определению вероятности, вероятность того, что наудачу взятые три шара окажутся красными, будет составлять $P(A) = \dfrac{120}{19600} = \dfrac{3}{490}$ .