Если открыть одновременно две трубы, то бассейн будет наполнен за 12 ч. Если сначала наполнять бассейн только через первую трубу в течение 5 ч, а затем только через вторую течение 9 часов, то водой будет наполнен половину бассейна. За сколько часов может наполнить бассейн каждая труба, работая самостоятельно?
ответ: 16 и 48 часов соответственно
Объяснение:
1 - емкость бассейна;
x - скорость наполнения первой трубы;
y - скорость наполнения второй трубы;
наполнение первой трубой: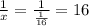
часов;
наполнение второй трубой: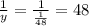
часов.