F(x) =3^x

Перечислите основные свойства функций и постройте их графии
РЕШИТЬ

Показать ответ

Ответ:

Лубаша

16.10.2020 22:52

Задание 3

График построен, во вложениях.

Чтобы построить у себя график по этой картинке и функции, сначала построим первый кусочек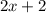 2x+2 - прямая.

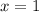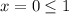Для этого надо выбрать две точки. Первая точка будет для x = 1 , как для граничного значения. Вторая при $x = 0 \leq 1$ .

Получили точки (1; 4), (0; 2). Откладываем эти точки на координатной плоскости и проводим луч от (1; 4) через точку (0; 2).

Теперь перейдем к 3 кусочку - прямой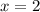 x = 2 . Он задан от 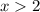x 2 . Это прямая, параллельная оси OX. Ставим точку граничного условия (2; 2), выбираем любой 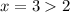x = 3 2 получаем вторую точку (3; 2). Проводим луч от (2; 2) через (3; 2).

Осталось провести гиперболу между (1; 4) и (2; 2), делаем её похожей на картинку во вложениях.

Задание 4

y = ax^2 + bx - 4

A = (-3; 8) , B = (1; 4)

Поставляем точки в выражение и получаем систему:

$\begin{equation*} \begin{cases} 9a - 3b -4 = 8 \\ a + b - 4 = 4 \end{cases}\end{equation*}\Leftrightarrow \begin{equation*} \begin{cases} 9a - 3b = 12 \\ a + b = 8 \end{cases}\end{equation*}\Leftrightarrow \begin{equation*} \begin{cases} 3a - b = 4 \\ a + b = 8 \end{cases}\end{equation*}\Leftrightarrow \begin{equation*} \begin{cases} 3a - b = 4 \\ (3+1)a + (1-1)b = 4+8 \end{cases}\end{equation*}$ $\Leftrightarrow \begin{equation*} \begin{cases} 3a - b = 4 \\ 4a = 12 \end{cases}\end{equation*}\Leftrightarrow \begin{equation*} \begin{cases} 3a - b = 4 \\ a = 3 \end{cases}\end{equation*}\Leftrightarrow \begin{equation*} \begin{cases} 3*3 - b = 4 \\ a = 3 \end{cases}\end{equation*}\Leftrightarrow \begin{equation*} \begin{cases} b = 9 - 4 \\ a = 3 \end{cases}\end{equation*}$

$\begin{equation*} \begin{cases} b = 5 \\ a = 3 \end{cases}\end{equation*}$

$\begin{equation*}y = 3x^2 + 5x - 4\end{equation*}$ - ответ

0,0(0 оценок)

Ответ:

menyaylo56

29.03.2020 16:47

$\left(\dfrac{1}{4};\;\dfrac{1}{3}\right]$

Объяснение:

Рассмотрим сначала первое неравенство системы.

Начнем с ОДЗ:

$log_3^2x+10,\;=\;x0\\log_3x+30,\;x\dfrac{1}{27}\\x0\\x+5\ne0,\;=\;x\ne-5\\=x\in\left(\dfrac{1}{27};+\infty\right)$

Продолжим решение:

$\dfrac{lg(log_3^2x+1)-lg(log_3x+3)}{x+5}\ge0\\\dfrac{lg\left(\dfrac{log_3^2x+1}{log_3x+3}\right)}{x+5}\ge0$

$lg\left(\dfrac{log_3^2x+1}{log_3x+3}\right)=0,\;=\;\dfrac{log_3^2x+1}{log_3x+3}=1\\\\=log_3^2x+1=log_3x+3,\;=\;log_3^2x-log_3x-2=0$

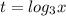Замена: t=log_3x .

$t^2-t-2=0\\t^2+t-2t-2=0\\t(t+1)-2(t+1)=0\\(t+1)(t-2)=0\\t=-1\\t=2$

Обратная замена:

$log_3x=-1\\x=\dfrac{1}{3}\\\\log_3x=2\\x=9$

С учетом ОДЗ оба корня подходят.

$x+5\ne0\\x\ne-5$

С учетом ОДЗ получим, что решение неравенства:

$x\in\left(\dfrac{1}{27};\;\dfrac{1}{3}\right]\cup[9;\;+\infty)$

Теперь перейдем ко второму неравенству системы:

Понятно, что сначала нужно написать ОДЗ.

$0.5x0,\;=\;x0\\(0.5x)^{6^x}0,\;=\;x0\\=x0$

Продолжим решение:

$36^x+36\sqrt[4]{6}-6^{x+\frac{1}{4}}$

Заметим, что данное неравенство хорошо раскладывается на множители:

$36^x+36\sqrt[4]{6}-6^{x+\frac{1}{4}}$

Решим неравенство по методу интервалов.

$\sqrt[4]{6}-6^x=0\\6^x=6^{\frac{1}{4}}\\x=\dfrac{1}{4}$

$36-6^x-log_60.5x=0\\log_60.5x=-6^x+36$

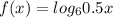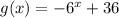Введем функции f(x)=log_60.5x и g(x)=-6^x+36 . Заметим, что первая функция возрастает, а вторая убывает. Поэтому, если уравнение имеет корень, он единственный. Теперь заметим, что x=2 - корень уравнения. Действительно, 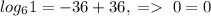$log_61=-36+36,\;=\;0=0$ , верно. Так, мы решили это уравнение, получив, что его корень x=2.