Хорошим будем называть натуральное число, все цифры которого (в десятичной записи) различные, идут в порядке возрастания, считая от разряда единиц к старшим разрядам, и среди
которых нет четырех идущих подряд (например, 3, 4, 5 и 6 не должны присутствовать в хорошем
числе одновременно). Сколько существует хороших чисел, записываемых цифрами от 1 до 8? Желательно с объяснением решения
Посчитаем сначала количество чисел, записываемых цифрами от до
до 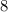 , а затем из этого числа вычтем те, среди которых есть четыре идущих подряд. Сразу заметим, что если в таком числе есть четыре подряд идущих числа, то и в самом числе они должны идти подряд.
, а затем из этого числа вычтем те, среди которых есть четыре идущих подряд. Сразу заметим, что если в таком числе есть четыре подряд идущих числа, то и в самом числе они должны идти подряд.
Выпишем числа от до
до 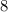 :
: 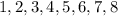 . Любые
. Любые 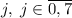 вычеркнутых цифры оставят число, в котором цифры идут по возрастанию. Наоборот, любое такое число может быть получено описанной операцией. Число вычеркнуть:
вычеркнутых цифры оставят число, в котором цифры идут по возрастанию. Наоборот, любое такое число может быть получено описанной операцией. Число вычеркнуть: 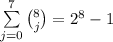 .
.
Теперь посчитаем количество тех, в которых есть четыре подряд идущих. В этом случае мы можем вычеркивать только из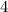 -ех оставшихся чисел. Поскольку четверок подряд идущих
-ех оставшихся чисел. Поскольку четверок подряд идущих 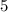 , то всего искомых чисел
, то всего искомых чисел 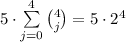 .
.
Итого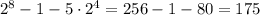 .
.