Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 16 км/ч, а вторую половину пути проехал со скоростью 96 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 57 км/ч. ответ дайте в км/ч.
Пусть х км/ч - скорость первого автомобиля, тогда скорость, с которой второй проехал первую половину пути, равна (х-16) км/ч. Расстояние между А и В обозначим S км. Время в пути равно или часов. Составим и решим уравнение:
Скорость Время Расстояние
По теч. ? 7ч
132км
Против ? 6ч
Vтеч.= ? Vсоб=10км/ч
Пусть х км/ч скорость течения реки,
(10+х) км/ч скорость лодки по течению, (10-х) км/ч скорость лодки против течения, 7*(10+х) км лодка по течению
6*(10-х) км против течения, т.к за все время путешествия лодка км, тогда составим уравнение:
7*(10+х)+ 6*(10-х)=132
70+7х+60-6х=132
х=132-130
х=2
2 км/ч скорость течения реки
Условие дано с ошибкой. Правильно звучит так:
Из А в В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 16 км/ч, а вторую половину пути проехал со скоростью 96 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 57 км/ч. ответ дайте в км/ч.
Пусть х км/ч - скорость первого автомобиля, тогда скорость, с которой второй проехал первую половину пути, равна (х-16) км/ч. Расстояние между А и В обозначим S км. Время в пути равно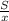
или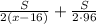 
часов. Составим и решим уравнение:
по теореме Виета:
ответ: скорость первого автомобиля 64 км/ч.