К данному уравнению x−y=3 подбери из предложенных уравнений второе уравнение так, чтобы полученная система не имела решений:

ответ (можно получить, используя построение):
y+x=−3
y=x+2
2x−y=6

Прямые x−y=3 и y+x=−3 будут (параллельны, совпадать, пересекаться)

Пример №1 (б):

(в скобках приведем разность и вычитаемое к общему знаменателю)

(дробь за скобкой перевернем, заменив тем самым деление на умножение)

(раскроем скобки)

(в дроби за скобкой числитель свернем по формуле квадрата разности, а в знаменателе этой дроби вынесем общий множитель 4z^2 за скобку)

(приведём подобные в числителе первой дроби)

(сократим в знаменателе первой дроби (3z-2) и в числителе второй дроби (3z-2))

(в числителе первой дроби вынесем общий множитель -12z за скобку)

(сократим -12z в числителе первой дроби и 4z^2 в знаменателе второй дроби на 4z)

(сократим (z+1) в числителе первой дроби и (z+1) в знаменателе второй дроби)

(раскроем скобки в числителе и знаменателе дроби соответственно)

(раскроем скобки)

ответ: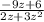

Пример №2 (в):

(в первой скобке приведем две дроби к общему знаменателю)

(во второй скобке приведем две дроби к общему знаменателю)

(раскроем скобки и приведем подобные в числителе первой дроби)

(приведем подобные в числителе второй дроби)

(вынесем общий множитель 3 в числителе первой дроби)

(сократим знаменатель первой дроби (u+3) и числитель второй дроби (u+3))

(сократим числитель первой дроби и знаменатель второй дроби на 3)

(сократим (u-3) в числителе первой дроби и (u-3) в знаменателе второй дроби)

ответ: 1

1.

8!/(8-6)!=(8*7*6*5*4*3*2*1)/(2*1)=8*7*6*5*4*3=2400

2*1=2

2400*2=4800

2.

15!/(15-5)!=15!/10!=15*14*13*12*11

14!/(14-5)!=14!/9!=14*13*12*11*10

14!/(14-4)!=14!/10!=14*13*12*11

(15*14*13*12*11-14*13*12*11*10)/(14*13*12*11)=((14*13*12*11)*(15-10))/(14*13*12*11)=15-10=5

3.

20!=20*19*18*17*16*15*14*13*12*11*10*9*8*7*6*5*4*3*2*1

20!/(20-5)=20!/15!=(20*19*18*17*16*15*14*13*12*11*10*9*8*7*6*5*4*3*2*1)/(15*14*13*12*11*10*9*8*7*6*5*4*3*2*1)=20*19*18*17*16

20!/(20-15)!=20!/5!=(20*19*18*17*16*15*14*13*12*11*10*9*8*7*6*5*4*3*2*1)/(5*4*3*2*1)=20*19*18*17*16*15*14*13*12*11*10*9*8*7*6

(20*19*18*17*16*15*14*13*12*11*10*9*8*7*6*5*4*3*2*1)/(20*19*18*17*16*15*14*13*12*11*10*9*8*7*6)=5*4*3*2*1=20*6=120