Приделении на 3 может получиться только три разных остатка: 0, 1 и 2.
Очевидно, что если поставить подряд два числа, у которых при делении на 3 получаются остатки 1 и 2, то их сумма разделится нацело на 3.
Три одинаковых остатка также подряд стоять не могут, потому что тогда их сумма кратна 3.
Значит в любой тройке идущих подряд чисел должно быть:
1) два числа с одинаковыми остатками и число с остатком 0
либо
2) два числа с остатком 0 и одно с ненулевым остатком.
Так как вопрос стоял о минимуме, то наш случай - под номером 1. То есть кратно трём каждое третье число.
ответ: 15.
Объяснение:
ответ: 1/6
Объяснение: для начала выведем формулу самой прямой.
Пусть прямая, проходящая через заданные точки, имеет вид у = kx + b.
По условию y(1) = 0, y(0) = -3.
1)1 · k + b =0, k + b = 0 ⇒ k = -b.
2)0·k + b = -3. b = -3 ⇒ k = 3.
Исходная прямая - y = 3x - 3.
Теперь исследуем функцию y = -x² + 4x - 3. График - парабола, ветви направлены вниз.
Нули функции - x = 1 и x = 3. Вершина: x = -b/2a = -4/-2=2, y=-2²+8-3=-4+5=1. (2; 1) Нам этого достаточно.
Строим графики (во вложении. Фигура, площадь которой нужно найти, заштрихована красным).
Площадь фигуры будем искать на отрезке [0; 1]
По формуле где f(x) ≥ g(x) (т.е. график функции f выше графика функции g) находим искомую площадь:
Искомая площадь - S = 1/6 (кв. ед)
Приделении на 3 может получиться только три разных остатка: 0, 1 и 2.
Очевидно, что если поставить подряд два числа, у которых при делении на 3 получаются остатки 1 и 2, то их сумма разделится нацело на 3.
Три одинаковых остатка также подряд стоять не могут, потому что тогда их сумма кратна 3.
Значит в любой тройке идущих подряд чисел должно быть:
1) два числа с одинаковыми остатками и число с остатком 0
либо
2) два числа с остатком 0 и одно с ненулевым остатком.
Так как вопрос стоял о минимуме, то наш случай - под номером 1. То есть кратно трём каждое третье число.
ответ: 15.
Объяснение:
ответ: 1/6
Объяснение: для начала выведем формулу самой прямой.
Пусть прямая, проходящая через заданные точки, имеет вид у = kx + b.
По условию y(1) = 0, y(0) = -3.
1)1 · k + b =0, k + b = 0 ⇒ k = -b.
2)0·k + b = -3. b = -3 ⇒ k = 3.
Исходная прямая - y = 3x - 3.
Теперь исследуем функцию y = -x² + 4x - 3. График - парабола, ветви направлены вниз.
Нули функции - x = 1 и x = 3. Вершина: x = -b/2a = -4/-2=2, y=-2²+8-3=-4+5=1. (2; 1) Нам этого достаточно.
Строим графики (во вложении. Фигура, площадь которой нужно найти, заштрихована красным).
Площадь фигуры будем искать на отрезке [0; 1]
По формуле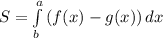
где f(x) ≥ g(x) (т.е. график функции f выше графика функции g) находим искомую площадь:
Искомая площадь - S = 1/6 (кв. ед)