Пусть v км/ч - начальная скорость поезда. Тогда время t, за которое поезд должен был пройти расстояние между станциями А и В, составляет t=54/v ч. По условию, расстояние 14 км поезд со скоростью v, поэтому ему на это потребовалось время t1=14/v ч. Оставшуюся часть пути, то есть 54-14=40 км, поезд по условию со скоростью v+10 км/ч, на что ему потребовалось время t2=40/(v+10) ч.
По условию, t1+t2=t+1/30-1/6=t-2/15=54/v-2/15 ч. Отсюда следует уравнение 14/v+40/(v+10)=54/v-2/15, которое приводится к квадратному уравнению v²+10*v-3000=0. Оно имеет корни v1=50 км/ч и v2=-60 км/ч, но так как v>0, то второй корень не годится и тогда v=50 км/ч.
6) 2ab - 2ac + 3b - 3c = 2ab + 3b - 2ac - 3c = b(2a+3) - c(2a+3) = (b-c)(2a+3)
7) 5ax + 10ay + bx + 2by = x(5a+b) + 2y(5a+b)= (5a+b)(2y+x)
8) 3ac + 6bc + 7ax +14bx= 3c(a+2b) + 7x(a+2b) = (3c+7x)(a+2b)
9) 2ax + 2xy - an - yn = 2x(a+y) - n(a+y) = (2x-n)(a+y)
10)
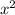+ xz + ax + az = x(x+z) + a(x+z) = (x+a)(x+z)
11) ax + 3ay + 5x + 15y= a(x+3y) + 5(x+3y) = (x+3y)(a+5)
12) 2bc + ac + 6b + 3a = c(2b+a) + 3(2b+a) = (2b+a)(3+a)
13) xy -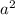
- ax + ay= x(y-a) - a(y-a) = (y-a)(x-a)
14) ab - ac -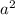
+ bc = a(b-a) - c(b-a)= (b-a)(a-c)
15)
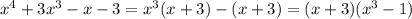далее разложение, если знаешь формулу разности кубов ---------------------------------
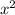(x+3)(x-1)(
+x+1)
ответ: 50 км/ч.
Объяснение:
Пусть v км/ч - начальная скорость поезда. Тогда время t, за которое поезд должен был пройти расстояние между станциями А и В, составляет t=54/v ч. По условию, расстояние 14 км поезд со скоростью v, поэтому ему на это потребовалось время t1=14/v ч. Оставшуюся часть пути, то есть 54-14=40 км, поезд по условию со скоростью v+10 км/ч, на что ему потребовалось время t2=40/(v+10) ч.
По условию, t1+t2=t+1/30-1/6=t-2/15=54/v-2/15 ч. Отсюда следует уравнение 14/v+40/(v+10)=54/v-2/15, которое приводится к квадратному уравнению v²+10*v-3000=0. Оно имеет корни v1=50 км/ч и v2=-60 км/ч, но так как v>0, то второй корень не годится и тогда v=50 км/ч.