В квадратном уравнение , которое имеет корни, обратные корням
квадратного уравнения , меняются местами коэффициенты и ,
причём .
Запишем данное уравнение в более удобном виде:
ax^2+bx+c=0; (предполагается, что а=/=0)
Теорема Виета:
x1*x2=c/a,
x1+x2=-b/a.
Новое уравнение ищем в виде:
Ax^2+Bx+C=0
Опять Виет: (при условии, что с=/=0)
C/A=1/x1*1/x2=1/(x1*x2)=a/c, отсюда C=(a/c)*A
-B/A=1/x1+1/x2=(x2+x1)/(x1*x2)=(-b/a)/(c/a)=-b/c, отсюда B=(b/c)*A
Итак, Ax^2+(b/c)*Ax+(a/c)*A=0, и окончательно:
cx^2+bx+a=0
В квадратном уравнение , которое имеет корни, обратные корням
, которое имеет корни, обратные корням
квадратного уравнения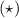 , меняются местами коэффициенты
, меняются местами коэффициенты  и
и  ,
,
причём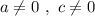 .
.
Запишем данное уравнение в более удобном виде:
ax^2+bx+c=0; (предполагается, что а=/=0)
Теорема Виета:
x1*x2=c/a,
x1+x2=-b/a.
Новое уравнение ищем в виде:
Ax^2+Bx+C=0
Опять Виет: (при условии, что с=/=0)
C/A=1/x1*1/x2=1/(x1*x2)=a/c, отсюда C=(a/c)*A
-B/A=1/x1+1/x2=(x2+x1)/(x1*x2)=(-b/a)/(c/a)=-b/c, отсюда B=(b/c)*A
Итак, Ax^2+(b/c)*Ax+(a/c)*A=0, и окончательно:
cx^2+bx+a=0