Мал, линия 3 : 1 Решите уравнение: 2 m 17 5 5 Запишите ответ в виде целого числа или десятичной дроби (если ответ содержит несколько чисел, разделите их точкой с за целое число или десятичная дробь сообщение утыра : 1 Решите уравнение :
(Таке завдання є вкрай некоректним) адже не сказано який куб має бути найменшим , чи найбільшим.
Зробимо так:
поріжемо даний паралелепіпед на кубіки в якого сторони рівні 1см. тоді уявляй перший ряд таких кубіків буде 20, и вкладеться 12 рядів в перший "поверх" і таких поверхів буде 24
20*12*24=5760 сантиметрових кубиків .
а якщо б ми ті кубики зробили ще меншими? - тому задачка погано обумовлена - але більше 5 тис кубиків ми нарізали - нарізали, тому - то є теж рішення
Малая теорема Ферма гласит, что для любого простого числа и натурального числа , где , справедливо равенство:
Найдем:
Заметим, что число 13 простое, причем 7<13, тогда можно применить малую теорему Ферма:
Другими словами:
, где - натуральное число
Заметим, что в биноме Ньютона все члены, кроме члена , помножены на некоторую степень числа 13, а значит данное выражение дает при делении на 13 остаток 1.
Найдем:
Число 11 простое, и 7<11, тогда рассуждая аналогично имеем:
Відповідь:
5760 сантиметрових кубиків
Пояснення:
нехай а=20см
b=12cм і с=24см
(Таке завдання є вкрай некоректним) адже не сказано який куб має бути найменшим , чи найбільшим.
Зробимо так:
поріжемо даний паралелепіпед на кубіки в якого сторони рівні 1см. тоді уявляй перший ряд таких кубіків буде 20, и вкладеться 12 рядів в перший "поверх" і таких поверхів буде 24
20*12*24=5760 сантиметрових кубиків .
а якщо б ми ті кубики зробили ще меншими? - тому задачка погано обумовлена - але більше 5 тис кубиків ми нарізали - нарізали, тому - то є теж рішення
ответ: 1
Объяснение:
Добрый вечер!
Заметим, что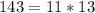
Малая теорема Ферма гласит, что для любого простого числа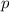 и натурального числа
и натурального числа 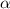 , где
, где 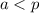 , справедливо равенство:
, справедливо равенство:
Найдем: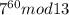
Заметим, что число 13 простое, причем 7<13, тогда можно применить малую теорему Ферма:
Другими словами:
Заметим, что в биноме Ньютона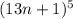 все члены, кроме члена
все члены, кроме члена 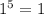 , помножены на некоторую степень числа 13, а значит данное выражение дает при делении на 13 остаток 1.
, помножены на некоторую степень числа 13, а значит данное выражение дает при делении на 13 остаток 1.
Найдем: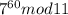
Число 11 простое, и 7<11, тогда рассуждая аналогично имеем:
Таким образом :