Мяч брошен вертикально вверх с начальной скоростью 24м/с зависимость расстояния h(в метрах) от мяча до земли от времени полёта выражается формулой h=24t-5t^2 1)какой наибольшей высоты достигае мяч? 2)через сколько секунд после броска мяч упадает на землю?
Понятно, что это квадратное уравнение. А когда квадратное уравнение будет иметь 2 различных отрицательных корня? Правильно, когда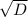
>-b, в данном случае b-коэффициент перед x.
Приступаем к решениею, приведем уравнение к приведенному(разделим на 2)
x^2+1,5x+0,5a=0
Найдём дискриминант
Т.к. в нашем уравнени b-отрицательное число (-1,5), то корню из дискриминанта достаточно принимать значения на промежутке
Потому что, если корень из дискриминанта будет больше 1,5 , то корни получатся либо положительными, либо равными нулю, а этого нам не надо.
Возведем обе части в квадрат, чтобы избавиться от корня
2,25-2a<2,25
-2a<0
a>0
Значит, мы получим 2 различных отрицательных корня, если a>0.
2) длины суммы двух векторов равна сумме их длин - неверно (верно, если только вектора коллинеарны (параллельны) и направлены в одну сторону).
Один из сложения векторов - правило треугольника. От конца одного вектора откладывается другой вектор. Тогда вектор, начало которого совпадает с началом первого вектора, а конец совпадет с концом второго вектора, будет суммой этих векторов.
3) сумма внутренних накрест лежащих углов при пересечении двух параллельных прямых секущей равна 180 градусов - неверно.
Внутренние накрест лежащие углы - это два угла во внутренней области параллельных прямых и на разных сторонах секущей. Они равны. Поэтому, равенство этих углов возможно в единственном случае, когда секущая перпендикулярна параллельным прямым.
4)длина окружности равна её удвоенному радиусу - неверно. Пропущено число пи.
5) площадь прямоугольника равна его периметру - неверно.
Площадь равна произведению сторон прямоугольника, а периметр - это сумма длин всех сторон.