Где и взаимнопростые натуральные числа. Для определенности будем считать, что .
Заметим, что числа простые. Из второго уравнения очевидно, что не делится на , то есть .
Предположим теперь, что , тогда , но тогда, поскольку сумма двух чисел делится на , то либо каждое из них делится на , либо не одно из них не делится на . Если каждое из них делится на , то делится на , но правая часть второго равенства делится только на первую степень числа . Если же оба из них не делятся на , то с учетом того, что , не делится на . То есть мы пришли к противоречию.
ответ: 43
Объяснение:
Пусть одно из чисел равно
, тогда второе 
.
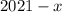Пусть:
Тогда:
Где
и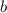 
взаимнопростые натуральные числа. Для определенности будем считать, что 
.
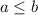Заметим, что числа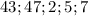
простые. Из второго уравнения очевидно, что 
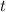не делится на 
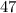, то есть 
.
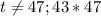Предположим теперь, что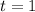
, тогда 
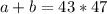, но тогда, поскольку сумма двух чисел делится на 
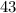, то либо каждое из них делится на 
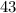, либо не одно из них не делится на 
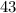. Если каждое из них делится на 
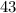, то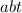 
делится на 
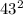, но правая часть второго равенства делится только на первую степень числа 
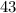. Если же оба из них не делятся на 
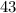, то с учетом того, что 
, 
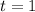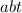не делится на 
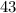. То есть мы пришли к противоречию.
Как видим, остается единственный вариант:
Объяснение:
Построить график функции
у=2×|х|+3
Шаг 1.
Строим график функции
у=|х|
Графиком являются биссектрисы
1 и 2 координатных четвертей.
Весь график расположен в верхней
полуплоскости.
Шаг 2.
Нужно изменить угол наклона вет
вей графика.
Построим и заполним таблицу:
у=2×|х|
х 0 -2 2
у 0 4 4
Строим график фунеции
у=2×|х|.
Шаг 3.
Строим график функции
у=2×|х|+3
График функции у=2×|х| поднимаем
вверх на 3 единицы ( совершаем па
раллельный перенос вдоль положи
тельного направления ОУ на 3ед. от
резка).
Построен искомый график.