На рисунке 8 изображен график некоторой функции. Пользуясь графиком найдите: 1) Значение функции y, если x=-5;-4,5;-2;-1;0;1;3;
2) Значения x, которым соответствует значение y=-2;-1,5;3;
3) Значения аргумента, при которых значение функции равно нулю;
4) Область определения и область значений функции.

На рисунке 8 изображен график некоторой функции. Пользуясь графиком найдите: 1) Значение функции y,

Показать ответ

Ответ:

volchica232005

24.03.2023 12:17

Объяснение:

Задачу можно решить различными .

. Первого игрока команды можно выбрать среди 15 спортсменов, то есть . Второго игрока команды можно выбрать среди оставшийся 14 спортсменов, то есть . Точно также, третьего игрока команды можно выбрать , четвёртого игрока команды можно выбрать , и наконец, пятого игрока команды можно выбрать .

Однако каждая команда при этом подсчете учтена несколько раз: одна и та же пятёрка спортсменов может быть выбрана по разному, например, сначала А, потом В, потом С, потом D, потом E, или сначала B, потом А, потом C, потом D, потом E и так далее. Поскольку число перестановок из пяти элементов равно 5!=120, то каждая команда учтена нами ровно 120 раз. Поэтому получается, что команду из 5 игроков можно выбрать

. Применим формулу комбинаторики.

Определение. Пусть имеется множество, содержащее n элементов. Произвольный неупорядоченный набор, состоящий из k различных элементов данного множества, называется сочетанием из n элементов по k элементов (или просто сочетанием из n по k).

Число сочетаний из n элементов по k элементов обозначается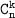 $\tt C_n^k$ и вычисляется по формуле:

$\displaystyle \tt C_n^k = \dfrac{n!}{k! \cdot (n-k)!} .$

Так как n = 15 и k = 5, то

$\displaystyle \tt C_{15}^5 = \dfrac{15!}{5! \cdot (15-5)!} =\dfrac{10! \cdot 11 \cdot 12 \cdot 13 \cdot 14 \cdot 15}{5! \cdot 10!} =\dfrac{11 \cdot 12 \cdot 13 \cdot 14 \cdot 15}{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5} =3003.$