На вступительном письменном экзамене по математике можно получить от 2 до Пятьдесят абитуриентов получили такие оценки:
2 2 7 8 9 4 5 7 10 6
6 6 7 9 10 2 2 2 3 4
4 5 7 9 6 2 3 10 4 2
5 7 6 9 10 10 2 2 4 6
3 2 6 7 7 8 7 5 6 6
а) Составить таблицу распределения данных и распределения частот в процентах.
б) Построить график распределения данных и столбчатую диаграмму частот в процентах.
в) Найти размах, моду и среднее измерение.
2. Какова вероятность того, что при двух последовательных бросаниях игрального кубика ни разу не выпадет шестерка?

рассмотрим первый группа средний рост 180 это средняя арифмитическая если предположить что группа состоит из 6 человек то сумма всех возрастов 180×6=1080  см если половина группы имеют минимальный рост 175 см то их суума равна 525 см значит на остальных отходит 1080-525=555 см на троих остальных то их рост равен 185 см если рассмотеть случай максимальной допустимой нормы то рост троих 190×3=570 см а значит на остальных отходит 1080-570=510 см 510÷3=170 а это значит при максимальной норме значение роста более приближенны рассмотрев взяв за моду крайние точки периода мы можем сделать вывод что годны 3/4 полка к службе

второй случай  максимальный рост 189 см это нам ничто не дает так как могут быть 150 см 160 см то есть условиям не подходящие а значит вторая группа вряд ли годна службе

третий случай медианна 176 но опять же нет гарантии что роста входят в этот промежуток

может ряд 150 160 176 195 200 а это значит что третий случай тоже не подойдет и всего этого только первыя группа годна службе

ответ 1 группа

Это функция представляет из себя ломанную, нам надо найти нули этой функции. На числовой прямой отметим точки в которых аргументы модулей равны нулю. Таким образом мы сможем узнать как на промежутках раскрываются модули и выглядит функция, сверху напишу модули, чтобы было понятно, хотя можно сразу писать конечную функцию для промежутка. см. вниз.

Да и ||2x-1|-5| я представил как |2x-6| и |-2x-4|, при этом первый существует когда x>0.5, а другой когда x<0.5 т.к. 2x-1=0 =>x=0.5

Ординаты точек в которых происходит смена знака у модуля.

Можно построить график ломанной, а можно сразу по условию определить где функция будет равна 0.

Главное помнить, что функция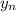 существует на каком-то промежутку, а не при всех х.

ответ: x∈[0.5;3].