Мы докажем это равенство по индукции. Но сначала преобразуем правую часть равенства к более удобному для нас виду:
А вот теперь применим индукцию. Легко проверить, что для n=1 равенство верно.
Теперь предположим что равенство верно для n=k:
Прибавив к обеим частям равенства получим:
Займёмся преобразованием правой части этого равенства:
Таким образом
То есть если равенство верно для произвольного n=k, то оно также оказывается верным и для n=k+1. По индукции заключаем верность равенства для любого натурального n.
Если же вас интересует каким можно вывести формулу, которую мы только что доказали - напишите мне в ЛС.
Заданная функция является квадратной, та как содержит квадрат переменной х. Графиком такой функции является парабола, ветви которой будут направлены вверх, так как перед квадратом х условно стоит знак «плюс».
Построить график такой функции можно подбором значений х и вычислением соответствующих значений функции у (это один из вариантов, самый простой), а также можно воспользоваться услугами построения графиков онлайн.
Подберем несколько координат точек, через которые пройдет данный график.
При х = 0 функция у(0) = 0^2 – 4 * 0 – 5 = –5 – точка (0; –5).
При х = 1 функция у(1) = 1^2 – 4 * 1 – 5 = –8 – точка (1; –8).
При х = –1 функция у(–1) = (–1)^2 – 4 * (–1) – 5 = 0 – точка (–1; 0).
При х = 2 функция у(2) = 2^2 – 4 * 2 – 5 = –9 – точка (2; –9).
При х = 3 функция у(3) = 3^2 – 4 * 3 – 5 = –8 – точка (3; –8).
При х = 4 функция у(4) = 4^2 – 4 * 4 – 5 = –5 – точка (4; –5).
При х = 5 функция у(5) = 5^2 – 4 * 5 – 5 = 0 – точка (5; 0).
Этих точек достаточно.
а) при х = 0,5 функция равна –6,75 – это можно проверить, подставив значение 0,5 вместо х в уравнение функции;
в) нули функции для промежутков у>0 и у<0;
г) промежуток, на котором функция будет возрастающей.
б) у = 3 при значениях х –1,5 и х = 5,5;
в) нулями функции есть точки (–1;0) и (5;0);
г) функция возрастает на промежутке, на котором х больше 2.
Объяснение:
Мы докажем это равенство по индукции. Но сначала преобразуем правую часть равенства к более удобному для нас виду:
Теперь предположим что равенство верно для n=k:
Прибавив к обеим частям равенства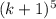 получим:
получим:
Займёмся преобразованием правой части этого равенства:
То есть если равенство верно для произвольного n=k, то оно также оказывается верным и для n=k+1. По индукции заключаем верность равенства для любого натурального n.
Если же вас интересует каким можно вывести формулу, которую мы только что доказали - напишите мне в ЛС.
Объяснение:
Заданная функция является квадратной, та как содержит квадрат переменной х. Графиком такой функции является парабола, ветви которой будут направлены вверх, так как перед квадратом х условно стоит знак «плюс».
Построить график такой функции можно подбором значений х и вычислением соответствующих значений функции у (это один из вариантов, самый простой), а также можно воспользоваться услугами построения графиков онлайн.
Подберем несколько координат точек, через которые пройдет данный график.
При х = 0 функция у(0) = 0^2 – 4 * 0 – 5 = –5 – точка (0; –5).
При х = 1 функция у(1) = 1^2 – 4 * 1 – 5 = –8 – точка (1; –8).
При х = –1 функция у(–1) = (–1)^2 – 4 * (–1) – 5 = 0 – точка (–1; 0).
При х = 2 функция у(2) = 2^2 – 4 * 2 – 5 = –9 – точка (2; –9).
При х = 3 функция у(3) = 3^2 – 4 * 3 – 5 = –8 – точка (3; –8).
При х = 4 функция у(4) = 4^2 – 4 * 4 – 5 = –5 – точка (4; –5).
При х = 5 функция у(5) = 5^2 – 4 * 5 – 5 = 0 – точка (5; 0).
Этих точек достаточно.
а) при х = 0,5 функция равна –6,75 – это можно проверить, подставив значение 0,5 вместо х в уравнение функции;
в) нули функции для промежутков у>0 и у<0;
г) промежуток, на котором функция будет возрастающей.
б) у = 3 при значениях х –1,5 и х = 5,5;
в) нулями функции есть точки (–1;0) и (5;0);
г) функция возрастает на промежутке, на котором х больше 2.