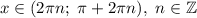Найди уравнение, равносильное уравнению x+4 корень x=-2 корень x-8 (корень x+3)^-1=0 (корень x-3)^-1=0 (корень x+3)^+1=0 (корень

В решении.

Объяснение:

Побудуйте графік функції у = 3(х – 2)2 за до геометричних перетворень. Підготуйте таблицю значень початкової функції у = х2, вибравши зручні для побудови значення аргументу.

Постройте график функции у = 3(х – 2)² с геометрических преобразований. Подготовьте таблицу значений начальной функции

у = х², выбрав удобные для построения значения аргумента.

График функции у = 3(х – 2)² парабола, получен при сдвиге классической параболы у = х² на две единицы вправо и "уже" её за счёт множителя 3.

Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.

Таблица:

х    0     1      2      3      4

у    12    3     0      3      12

По вычисленным точкам построить параболу.

Таблица значений начальной функции у = х²:

х    -3     -2     -1       0      1      2     3

у     9      4       1       0      1      4     9

Произведение двух выражений будет отрицательно, если они имеют разные знаки. Запишем совокупность двух систем:

Рассмотрим из второй системы неравенство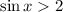 . Оно не имеет решений, так как синус принимает значения из отрезка . Значит, и вся вторая система не имеет решений.

В рассмотрении остается первая система, решения которой будут соответствовать решениям совокупности:

Рассмотрим неравенство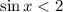 . Оно напротив выполняется при любых значениях по тем же причинам: синус принимает значения из отрезка .

Тогда, решение системы сводится к решению первого неравенства:

ответ: