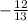Используя основное тригонометрическое тождество:
п<0<3п/2 находится в третьем координатном угле,там синус принимает
отрицательные значения, а значит ответ:
Найти: sinx
Решение:
sin²x+cos²x=1
sin²x=1 - cos²x
Т.к. α принадлежит III четверти, то sinx будет отрицательным =>
Используя основное тригонометрическое тождество:
п<0<3п/2 находится в третьем координатном угле,там синус принимает
отрицательные значения, а значит ответ: