99\3=33 всех 33 числа составим арифм прогрессию
а1=3 а2=а1+d=6 a33=3+3(33-1)=3+ 96=99 S33=(a1+a33)*33\2
S33=102*33\2=1683
Данные числа являются арифметической прогрессией, где а₁=3; а₃₃=99. Соответственно d=3.((99-3)/32).
Сумма членов арифметической прогрессии равна . В данном случае .
Значит = = 1683.
ответ: 1683.
99\3=33 всех 33 числа составим арифм прогрессию
а1=3 а2=а1+d=6 a33=3+3(33-1)=3+ 96=99 S33=(a1+a33)*33\2
S33=102*33\2=1683
Данные числа являются арифметической прогрессией, где а₁=3; а₃₃=99. Соответственно d=3.((99-3)/32).
Сумма членов арифметической прогрессии равна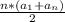
. В данном случае 
.
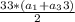Значит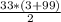
= 
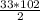= 1683.
ответ: 1683.