1. да
2. нет
3. да
4. да
5. нет
6. нет
7. нет
8. нет
9.нет
Объяснение:
Натуральные числа
Это числа, которые используются при счете: 1, 2, 3... и т.д.
Ноль не является натуральным.
Натуральные числа принято обозначать символом N.
Целые числа. Положительные и отрицательные числа
Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Рациональные числа
Это конечные дроби и бесконечные периодические дроби . Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.
Иррациональные числа
Бесконечная непериодическая дробь называется иррациональным числом.
Множество иррациональных чисел обозначается J.
Действительные числа
Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.
Действительные числа обозначаются символом R.
Пример №1 (б):
(в скобках приведем разность и вычитаемое к общему знаменателю)
(дробь за скобкой перевернем, заменив тем самым деление на умножение)
(раскроем скобки)
(в дроби за скобкой числитель свернем по формуле квадрата разности, а в знаменателе этой дроби вынесем общий множитель 4z^2 за скобку)
(приведём подобные в числителе первой дроби)
(сократим в знаменателе первой дроби (3z-2) и в числителе второй дроби (3z-2))
(в числителе первой дроби вынесем общий множитель -12z за скобку)
(сократим -12z в числителе первой дроби и 4z^2 в знаменателе второй дроби на 4z)
(сократим (z+1) в числителе первой дроби и (z+1) в знаменателе второй дроби)
(раскроем скобки в числителе и знаменателе дроби соответственно)
ответ:
Пример №2 (в):
(в первой скобке приведем две дроби к общему знаменателю)
(во второй скобке приведем две дроби к общему знаменателю)
(раскроем скобки и приведем подобные в числителе первой дроби)
(приведем подобные в числителе второй дроби)
(вынесем общий множитель 3 в числителе первой дроби)
(сократим знаменатель первой дроби (u+3) и числитель второй дроби (u+3))
(сократим числитель первой дроби и знаменатель второй дроби на 3)
(сократим (u-3) в числителе первой дроби и (u-3) в знаменателе второй дроби)
ответ: 1
1. да
2. нет
3. да
4. да
5. нет
6. нет
7. нет
8. нет
9.нет
Объяснение:
Натуральные числа
Это числа, которые используются при счете: 1, 2, 3... и т.д.
Ноль не является натуральным.
Натуральные числа принято обозначать символом N.
Целые числа. Положительные и отрицательные числа
Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Рациональные числа
Это конечные дроби и бесконечные периодические дроби . Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.
Иррациональные числа
Бесконечная непериодическая дробь называется иррациональным числом.
Множество иррациональных чисел обозначается J.
Действительные числа
Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.
Действительные числа обозначаются символом R.
Пример №1 (б):
(в скобках приведем разность и вычитаемое к общему знаменателю)
(дробь за скобкой перевернем, заменив тем самым деление на умножение)
(раскроем скобки)
(в дроби за скобкой числитель свернем по формуле квадрата разности, а в знаменателе этой дроби вынесем общий множитель 4z^2 за скобку)
(приведём подобные в числителе первой дроби)
(сократим в знаменателе первой дроби (3z-2) и в числителе второй дроби (3z-2))
(в числителе первой дроби вынесем общий множитель -12z за скобку)
(сократим -12z в числителе первой дроби и 4z^2 в знаменателе второй дроби на 4z)
(сократим (z+1) в числителе первой дроби и (z+1) в знаменателе второй дроби)
(раскроем скобки в числителе и знаменателе дроби соответственно)
(раскроем скобки)
ответ: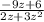
Пример №2 (в):
(в первой скобке приведем две дроби к общему знаменателю)
(во второй скобке приведем две дроби к общему знаменателю)
(раскроем скобки и приведем подобные в числителе первой дроби)
(приведем подобные в числителе второй дроби)
(вынесем общий множитель 3 в числителе первой дроби)
(сократим знаменатель первой дроби (u+3) и числитель второй дроби (u+3))
(сократим числитель первой дроби и знаменатель второй дроби на 3)
(сократим (u-3) в числителе первой дроби и (u-3) в знаменателе второй дроби)
ответ: 1