Построим график квадратной функции методом "по 3 точкам", а именно по вершине параболы и двум её корням (дискриминант не отрицательный).
Это координаты вершины, почему именно такие? Корни уравнения:
, функция чётная (есть ось симметрии), и есть какая координата по оси Ох, которая меняется вправо и влево на одинаковое число.
Найдём нули функции:
Суть в том, что мы отмечаем три точки на координатной плоскости и проводим ветви параболы, осознавая как именно растёт функции, функции x^2, то есть не надо ветви проводить как будто это уравнение прямой.
И чтоб всё было отмечено, найдём точки пересечения функции с осью Оу: то есть (0;3)
1) При x∈(-∞;-1)∪(3;+∞) функция принимает отрицательные значения
При x∈(-1;3) функция принимает положительные значения
2) При x∈(-∞;1) функция растёт
При x∈(1;+∞) функция убывает
3) Минимальное значение -∞, достигается в точках (-∞;-∞) или (+∞;-∞)
Максимальное значение 4, достигается в точке (1;4)
я конечно не знаю правильно или неправильно. ну вот короче мое решение:
арбуз( основа все слово и корень все слово, нулевое окончание)
малина( основа малин, корень- малин, окончание-а).
дежурный( основа- дежурн, окончание-ый, корень-дежур и вроде суффикс-н)
ученик(основа- ученик, нулевое окончание, корень- учен, суффикс-ик.)
учитель( вроде корень и основа- учитель и нулевое окончание)
( основа- , корень- и окончание-а)
пенал(основа- пенал, корень-пенал и нулевое окончание)
тетради( основа- тетрад, корень- тетрад, окончание-и)
ягоды ( основа- ягод, корень- ягод, окончание-ы)
лопата( корень-лопат, основа- лопат и окончание-а)
москва( основа-москв, корень-москв, окончание-а)
левочка( основа-лавочк, корень-лав, суффикс-очк, окончание-а)
молоко ( основа- молок, корень-молок, и окончание- о)
урожай -
слова иностранные и поэтому их сложно разбирать.
Построим график квадратной функции методом "по 3 точкам", а именно по вершине параболы и двум её корням (дискриминант не отрицательный).
Это координаты вершины, почему именно такие? Корни уравнения:
Найдём нули функции:
Суть в том, что мы отмечаем три точки на координатной плоскости и проводим ветви параболы, осознавая как именно растёт функции, функции x^2, то есть не надо ветви проводить как будто это уравнение прямой.
И чтоб всё было отмечено, найдём точки пересечения функции с осью Оу: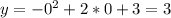
то есть (0;3)
1) При x∈(-∞;-1)∪(3;+∞) функция принимает отрицательные значения
При x∈(-1;3) функция принимает положительные значения
2) При x∈(-∞;1) функция растёт
При x∈(1;+∞) функция убывает
3) Минимальное значение -∞, достигается в точках (-∞;-∞) или (+∞;-∞)
Максимальное значение 4, достигается в точке (1;4)