, тогда . Получаем уравнение:
Из интервала :
Так как , то . Подставляем в корень уравнения:
.
Таким образом, из заданного интервала есть два таких значения: 0 и π.
Из интервала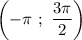 :
:
Так как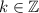 , то
, то 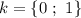 . Подставляем в корень уравнения:
. Подставляем в корень уравнения:
Таким образом, из заданного интервала есть два таких значения: 0 и π.