Поскольку необходимо представить число 68 в виде суммы двух чисел, то пусть первое число х, тогда второе число (68-х). Тогда сумма квадратов слагаемых будет равна: х²+(68-х)²=х²+68²-2*68*х+х²=2х²-136х+4624
Здесь можно найти минимальное значение 2-мя 1) с производной (2х²-136х+4624)'=4x-136 4x-136=0 4x=136 x=136:4 х=34 Значит будет 2 одинаковых положительных числа 34 и 34.
2) с графика y=2х²-136х+4624 Это парабола - ветви направлены вверх. Значит наименьшее значение будет в вершине параболы. х₀=-b/2a=-(-136)/4=34
Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2)
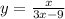. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б)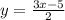
при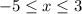 
Если x = -5, то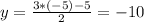
Если х= 3, то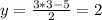
Значит,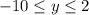
Тогда сумма квадратов слагаемых будет равна:
х²+(68-х)²=х²+68²-2*68*х+х²=2х²-136х+4624
Здесь можно найти минимальное значение 2-мя
1) с производной
(2х²-136х+4624)'=4x-136
4x-136=0
4x=136
x=136:4
х=34
Значит будет 2 одинаковых положительных числа 34 и 34.
2) с графика
y=2х²-136х+4624
Это парабола - ветви направлены вверх. Значит наименьшее значение будет в вершине параболы.
х₀=-b/2a=-(-136)/4=34
34+34=68