x = 0 не является корнем уравнения (-729 ≠ 0). Значит, можно поделить на x³:
Пусть . Тогда
Выполним замену:
Представим t в виде суммы двух действительных чисел: t = b + c. Заметим, что
При подстановке t = b + c мы действительно получим 0 (чтобы убедиться в этом, достаточно проделать действия в обратном порядке), то есть t = b + c является корнем такого уравнения. Попробуем найти такие b и c, чтобы при подстановке этих чисел в последнее уравнение коэффициент перед t был равен -6, а свободный коэффициент был равен 6. Так мы получим нужное уравнение, но заодно и найдём его корень:
Решим второе уравнение. b ≠ 0, иначе это противоречило бы первому уравнению (0 ≠ 2). Домножим на b³ и сделаем замену b³ = z:
По теореме Виета
В первом случае , во втором — . Они отличаются только перестановкой слагаемых, поэтому это один и тот же корень. Получаем:
Объяснение:
x = 0 не является корнем уравнения (-729 ≠ 0). Значит, можно поделить на x³:
Пусть . Тогда
. Тогда
Выполним замену:
Представим t в виде суммы двух действительных чисел: t = b + c. Заметим, что
При подстановке t = b + c мы действительно получим 0 (чтобы убедиться в этом, достаточно проделать действия в обратном порядке), то есть t = b + c является корнем такого уравнения. Попробуем найти такие b и c, чтобы при подстановке этих чисел в последнее уравнение коэффициент перед t был равен -6, а свободный коэффициент был равен 6. Так мы получим нужное уравнение, но заодно и найдём его корень:
Решим второе уравнение. b ≠ 0, иначе это противоречило бы первому уравнению (0 ≠ 2). Домножим на b³ и сделаем замену b³ = z:
По теореме Виета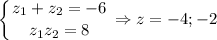
В первом случае![t=-\sqrt[3]{4}-\sqrt[3]{2}](/tpl/images/2009/2628/2c72b.png) , во втором —
, во втором — ![t=-\sqrt[3]{2}-\sqrt[3]{4}](/tpl/images/2009/2628/5f922.png) . Они отличаются только перестановкой слагаемых, поэтому это один и тот же корень. Получаем:
. Они отличаются только перестановкой слагаемых, поэтому это один и тот же корень. Получаем: