Заметим, что дает такой же остаток при делении на s, что и . (Доказывается, например, так. Раскрываем скобки:
Очевидно, на каждом шаге будет образовываться слагаемое, делящееся на qs, и степень умноженная на r. Все слагаемые первого типа на остаток не влияют, так что остается только )
Кроме того, остаток от деления от суммы равен остатку от деления от суммы остатков (as + b + cs + d = (a + c)s + (b + d) дает такой же остаток при делении на s, что и b + d), а так же произведение можно менять на произведение остатков
Заметим, что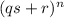 дает такой же остаток при делении на s, что и
дает такой же остаток при делении на s, что и 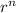 . (Доказывается, например, так. Раскрываем скобки:
. (Доказывается, например, так. Раскрываем скобки:
Очевидно, на каждом шаге будет образовываться слагаемое, делящееся на qs, и степень умноженная на r. Все слагаемые первого типа на остаток не влияют, так что остается только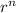 )
)
Кроме того, остаток от деления от суммы равен остатку от деления от суммы остатков (as + b + cs + d = (a + c)s + (b + d) дает такой же остаток при делении на s, что и b + d), а так же произведение можно менять на произведение остатков
Применяем наблюдения: