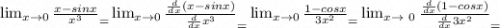Войти Регистрация Спроси ai-bota

найти предел, пользвуясь правилом Лопиталя(очень надо)

найти предел, пользвуясь правилом Лопиталя(очень надо)

Показать ответ

Ответ:

160678

18.12.2020 17:55

1) $\lim_{x \to \00} \frac{x-sinx}{x^3} _ = \lim_{x \to \00} \frac{\frac{d}{dx}(x-sinx) }{\frac{d}{dx}x^3 } _ = \lim_{x \to \00} \frac{1-cosx}{3x^2} _= \lim_{x \to \ 0} \frac{\frac{d}{dx}(1-cosx) }{\frac{d}{dx} 3x^2} _=$

$= \lim_{x \to \ 0} \frac{sinx}{6x} _= \lim_{x \to \ 0} \frac{\frac{d}{dx}sinx }{\frac{d}{dx} 6x} = \lim_{x \to \ 0} \frac{cosx}{6} _=\frac{cos0}{6} =\frac{1}{6} = 0,16$

0,0(0 оценок)

Популярные вопросы: Алгебра

DenneD432

16.02.2022 12:11

Моторная лодка против течения реки 91 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. найдите скорость течения, если скорость лодки...

1978dan

17.09.2022 07:06

кто понимает. Найдите производную функции f (x)=2x^2+sinx ...

ritailicheva0

08.10.2022 19:05

Решите рациональное неравенство заменой, распишите максимально подробно...

maria4231

06.06.2022 02:03

Уравнение касательной к параболе в некоторой точке y = 4 – 7 x . Определить значение производной в этой точке ....

svesda2

06.05.2023 21:45

Всё в корне 2 умножить на 45 умножить на 5...

abramov26ozzk18

04.08.2022 20:50

Установите соответствие между графиками функций и формулами, которые их задают....

serhius

10.05.2022 20:23

Решите уравнение 1(x−13)2−1x−13−6=0. (в первое окошко запиши меньший корень, в виде десятичной дроби; во второе окошко запиши больший корень, в виде неправильной дроби)...

kornienko123456

01.06.2020 22:20

У выражение: √11*3^6*√11*2^2...

Horoshist2287

01.06.2020 22:20

Решите уравнение 5x^2-9x+4=0 . Если уравнение имеет более одного корня, в ответ запишите меньший из корней....

nazmiburkanova7

08.11.2021 12:55

829/20+ 5,875+ 20 35/40 = решите надо...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку