Да я те отвечаю))Ну а сеьезно Значение неизвестной величиной, для которой из данного уравнения мы получим истинное числовое равенство, называется корнем этого уравнения. Два уравнения называются эквивалентными, если множества их корней совпадают, корни первого уравнения являются также корнями второго и наоборот. Действуют следующие правила: 1. Если в данном уравнении значение заменяется другим, но идентичным, мы получаем уравнение, эквивалентное данному. 2. Если в данном уравнении некоторое значение переносится из одной стороны на другую с противоположным знаком, мы получаем уравнение, эквивалентное (равное) заданному. 3. Если мы умножаем или делим обе стороны уравнения на одно и то же число, отличное от нуля, мы получаем уравнение, эквивалентное заданному. Уравнение вида ax + b = 0, где a, b - заданные числа, называется простым уравнением по отношению к неизвестной величине х.
Конечно же обе формулы дают ОДНИ И ТЕ ЖЕ решения. Просто запись в частном случае более лёгкая для восприятия.
Из этой формулы следует, что sinx=1 при х=П/2 , причём, если эту точку повернуть на один круг (+/-2П), два круга (+/-4П), три круга (+/-6П) и так далее, то придём в одну ту же точку В на тригонометрическом круге с декартовыми координатами (0,1) . Смотри рисунок. Поворачивать точку можно против часовой стрелки ( ) или по часовой стрелкe ( ) .
В случае общей формулы надо рассматривать чётные и нечётные значения .
Если k- чётно, то получаем
То есть получили ту же формулу, что и в частном случае.
Если k - нечётно, то получаем
На вид эта формула не похожа на частный случай, но точка х= -3П/2 получается из точки с дек. координатами А(1,0) путём её поворота на 270° (3П/2) по часовой стрелке (отрицательное направление поворота, поэтому знак (-) пишем ). И попадёт она в точку В(0,1). Но ведь мы попадём в точку В(0,1) и при повороте точки А(1,0) против часовой стрелки ( положительное направление поворота) на 90° (П/2) .
Поэтому запись равноценна записи .
Конечно, предпочтительнее сразу писать частный вид формулы для решения уравнения sinx=1, потому что он более простой в записи , но описывает те же решения, что и частный случай.
1. Если в данном уравнении значение заменяется другим, но идентичным, мы получаем уравнение, эквивалентное данному.
2. Если в данном уравнении некоторое значение переносится из одной стороны на другую с противоположным знаком, мы получаем уравнение, эквивалентное (равное) заданному.
3. Если мы умножаем или делим обе стороны уравнения на одно и то же число, отличное от нуля, мы получаем уравнение, эквивалентное заданному.
Уравнение вида ax + b = 0, где a, b - заданные числа, называется простым уравнением по отношению к неизвестной величине х.
Объяснение:
Конечно же обе формулы дают ОДНИ И ТЕ ЖЕ решения. Просто запись в частном случае более лёгкая для восприятия.
Из этой формулы следует, что sinx=1 при х=П/2 , причём, если эту точку повернуть на один круг (+/-2П), два круга (+/-4П), три круга (+/-6П) и так далее, то придём в одну ту же точку В на тригонометрическом круге с декартовыми координатами (0,1) . Смотри рисунок. Поворачивать точку можно против часовой стрелки (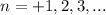
) или по часовой стрелкe (
) .
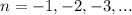В случае общей формулы надо рассматривать чётные и нечётные значения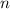
.
Если k- чётно, то получаем
То есть получили ту же формулу, что и в частном случае.
Если k - нечётно, то получаем
На вид эта формула не похожа на частный случай, но точка х= -3П/2 получается из точки с дек. координатами А(1,0) путём её поворота на 270° (3П/2) по часовой стрелке (отрицательное направление поворота, поэтому знак (-) пишем ). И попадёт она в точку В(0,1). Но ведь мы попадём в точку В(0,1) и при повороте точки А(1,0) против часовой стрелки ( положительное направление поворота) на 90° (П/2) .
Поэтому запись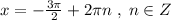
равноценна записи 
.
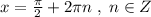Конечно, предпочтительнее сразу писать частный вид формулы для решения уравнения sinx=1, потому что он более простой в записи , но описывает те же решения, что и частный случай.