Скорее всего в условии ошибка. Представляю исправленное условие.
Произведение равно нулю в том случае, когда хотя бы один из множителей обращается к нулю.
Если же в условии все в порядке, то решение следующее.
Решим это кубическое уравнение методом Кардано
Поделим обе части последнего уравнения на 4
Здесь коэффициенты
Поскольку S > 0 то кубическое уравнение имеет три действительных корня
Скорее всего в условии ошибка. Представляю исправленное условие.
Произведение равно нулю в том случае, когда хотя бы один из множителей обращается к нулю.
Если же в условии все в порядке, то решение следующее.
Решим это кубическое уравнение методом Кардано
Поделим обе части последнего уравнения на 4
Здесь коэффициенты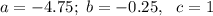
Поскольку S > 0 то кубическое уравнение имеет три действительных корня