(x+5)⁴-13x²(x+5)²+36x⁴=0 Для возведения в степерь воспользуемся биноминальной формулой x⁴+20x³+150x²+500x+625-13x⁴+130x³+325x²+36x⁴=0
24x⁴-110x³-175x²+500x+625=0 Разложим одночлены в сумму нескольких 24x⁴-110x³-275x²+100x²+500x+625=0 24x⁴-110x²(x+2.5)+100(x+2.5)²=0 Пусть x²=A, x+2.5=B, в результате 24A²-110AB+100B²=0 24A²-80AB-30AB+100B²=0 8A(3A-10B)-10B(3A-10B)=0 (3A-10B)(8A-10B)=0 Возвращаемся к замене (3x²-10(x+2.5))(8x²-10(x+2.5))=0 (3x²-10x-25)(8x²-10x-25)=0 Два уравнения 3x²-10x-25=0 D=b²-4ac=100+300=400 x₁=-5/3 x₂=5
8x²-10x-25=0 D=100+32*25=900 x₃=-1.25 x₄=2.5
ответ: -5/3; -1.25; 2.5; 5.
2(x-1)⁴-5(x²-3x+2)²+2(x-2)⁴=0 Биноминальна формула Раскроем скобки по формуле 2x⁴-8x³+12x²-8x+2-5x⁴+30x³-65x²+60x-20+2x⁴-16x³+48x²-64x+32=0 x⁴-6x³+5x²+12x-14=0 Пусть x²-3x=t, в результате замены переменных получаем уравнение t²-4t-14=0 D=b²-4ac=16+4*14=72 t₁=2-3√2 t₂=2+3√2 Вовзращаемся к замене x²-3x=2-3√2 x²-3x-(2-3√2)=0 D=17-12√2; √D=3-2√2 x₁=√2 x₂=3-√2
Для возведения в степерь воспользуемся биноминальной формулой
x⁴+20x³+150x²+500x+625-13x⁴+130x³+325x²+36x⁴=0
24x⁴-110x³-175x²+500x+625=0
Разложим одночлены в сумму нескольких
24x⁴-110x³-275x²+100x²+500x+625=0
24x⁴-110x²(x+2.5)+100(x+2.5)²=0
Пусть x²=A, x+2.5=B, в результате
24A²-110AB+100B²=0
24A²-80AB-30AB+100B²=0
8A(3A-10B)-10B(3A-10B)=0
(3A-10B)(8A-10B)=0
Возвращаемся к замене
(3x²-10(x+2.5))(8x²-10(x+2.5))=0
(3x²-10x-25)(8x²-10x-25)=0
Два уравнения
3x²-10x-25=0
D=b²-4ac=100+300=400
x₁=-5/3
x₂=5
8x²-10x-25=0
D=100+32*25=900
x₃=-1.25
x₄=2.5
ответ: -5/3; -1.25; 2.5; 5.
2(x-1)⁴-5(x²-3x+2)²+2(x-2)⁴=0
Биноминальна формула
Раскроем скобки по формуле
2x⁴-8x³+12x²-8x+2-5x⁴+30x³-65x²+60x-20+2x⁴-16x³+48x²-64x+32=0
x⁴-6x³+5x²+12x-14=0
Пусть x²-3x=t, в результате замены переменных получаем уравнение
t²-4t-14=0
D=b²-4ac=16+4*14=72
t₁=2-3√2
t₂=2+3√2
Вовзращаемся к замене
x²-3x=2-3√2
x²-3x-(2-3√2)=0
D=17-12√2; √D=3-2√2
x₁=√2
x₂=3-√2
x²-3x=2+3√2
x²-3x-(2+3√2)=0
D=17+12√2; √D=3+2√2
x₃=-√2
x₄=3+√2
ответ: ±√2; 3±√2.
Для решения запишем формулу бинома Ньютона:
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение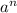
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение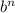
.
Рассмотрим многочлен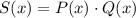
, где:
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена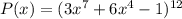
:
- степень определяется выражением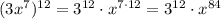
, то есть степень равна 84
- свободный член равен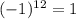
Для многочлена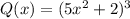
:
- степень определяется выражением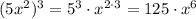
, то есть степень равна 6
- свободный член равен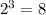
Наконец, для многочлена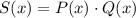
получим:
- степень определяется выражением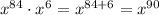
, то есть степень равна 90
- свободный член равен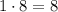
Сумма степени и свободного члена многочлена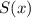
:
ответ: 98