Формула для суммы первых n членов геометрической прогрессии:
Sn = b₁·(q^n - 1)/(q - 1)
Для 8 членов геометрической прогрессии
S₈ = b₁·(q⁸ - 1)/(q - 1)
Формула для n-го члена геометрической прогрессии:
bn = b₁·q^(n-1)
n = 6 b₆ = b₁·q⁵
n = 4 b₄ = b₁·q³
n = 3 b₃ = b₁·q²
По условию:
b₆ - b₄ = 72
b₃ - b₁ = 9
или
b₁·q⁵ - b₁·q³ = 72
b₁·q² - b₁ = 9
Преобразуем эти выражения
b₁·q³·(q² - 1) = 72 (1)
b₁·(q² - 1) = 9 (2)
Разделим (1) на (2) и получим
q³ = 8, откуда
q = 2
Из (2) найдём b₁
b₁ = 9/(q² - 1) = 9/(4 - 1) = 3
Подставим q = 2 и b₁ = 3 в S₈ = b₁·(q⁸ - 1)/(q - 1)
S₈ = 3·(2⁸ - 1)/(2 - 1) = 3·(256 - 1) = 765
ответ: S₈ = 765
1) y' = y³x
Проинтегрируем обе части:
- общее решение дифф. уравнения.
Из начального условия y(1)=1 найдем частное решение:
Подставив в общее решение, найдем С
-1/2 = 1/2 + С ⇔ С = -1/4
- частное решение дифф. уравнения.
2)
Для начала найдем общее решение однородного дифф. уравнения
Проинтегрировав, получим:
ln|y|=3ln|x| + lnC
y = Cx³ - общее решение однородного дифф. уравнения
y = C(x)x³ подставим в наше дифф. уравнение
- общее решение дифф. уравнения
Из начального условия y(1) = e найдем C₁
C₁ = 0
- частное решение дифф. уравнения
Формула для суммы первых n членов геометрической прогрессии:
Sn = b₁·(q^n - 1)/(q - 1)
Для 8 членов геометрической прогрессии
S₈ = b₁·(q⁸ - 1)/(q - 1)
Формула для n-го члена геометрической прогрессии:
bn = b₁·q^(n-1)
n = 6 b₆ = b₁·q⁵
n = 4 b₄ = b₁·q³
n = 3 b₃ = b₁·q²
По условию:
b₆ - b₄ = 72
b₃ - b₁ = 9
или
b₁·q⁵ - b₁·q³ = 72
b₁·q² - b₁ = 9
Преобразуем эти выражения
b₁·q³·(q² - 1) = 72 (1)
b₁·(q² - 1) = 9 (2)
Разделим (1) на (2) и получим
q³ = 8, откуда
q = 2
Из (2) найдём b₁
b₁ = 9/(q² - 1) = 9/(4 - 1) = 3
Подставим q = 2 и b₁ = 3 в S₈ = b₁·(q⁸ - 1)/(q - 1)
S₈ = 3·(2⁸ - 1)/(2 - 1) = 3·(256 - 1) = 765
ответ: S₈ = 765
1) y' = y³x
Проинтегрируем обе части:
Из начального условия y(1)=1 найдем частное решение:
Подставив в общее решение, найдем С
-1/2 = 1/2 + С ⇔ С = -1/4
2)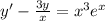
Для начала найдем общее решение однородного дифф. уравнения
Проинтегрировав, получим:
ln|y|=3ln|x| + lnC
y = Cx³ - общее решение однородного дифф. уравнения
y = C(x)x³ подставим в наше дифф. уравнение
Из начального условия y(1) = e найдем C₁
C₁ = 0