(см. объяснение)
Объяснение:
Введем функцию .
Заметим, что перед нами уравнение двух парабол, склеивающихся в фиксированной точке .
Этот график может ездить только вверх-вниз в зависимости от значений параметров и .
Уравнение может иметь ровно два корня при любом значении параметра только, если .
Тогда перейдем к неравенству:
Построим его в координатах .
(см. прикрепленный файл)
Получили, что при исходное уравнение имеет ровно два различных корня при любом значении параметра .
ответим теперь на вопрос задачи: ниже .
Задание выполнено!
(см. объяснение)
Объяснение:
Введем функцию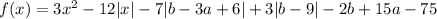 .
.
Заметим, что перед нами уравнение двух парабол, склеивающихся в фиксированной точке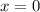 .
.
Этот график может ездить только вверх-вниз в зависимости от значений параметров и
и 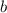 .
.
Уравнение может иметь ровно два корня при любом значении параметра
может иметь ровно два корня при любом значении параметра 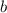 только, если
только, если 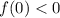 .
.
Тогда перейдем к неравенству:
Построим его в координатах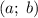 .
.
(см. прикрепленный файл)
Получили, что при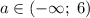 исходное уравнение имеет ровно два различных корня при любом значении параметра
исходное уравнение имеет ровно два различных корня при любом значении параметра 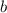 .
.
ответим теперь на вопрос задачи: ниже .
.
Задание выполнено!