Nonnoba ДІАГНОСТИЧНА РОБОТА ( 10 КЛАС) Варіант 1. 1. (0, ) Яка з наведених систем нерівностей не має розв'язку? А х> 3, х2-2; Б х<3, х2-2; B) х<3, x < -2; Г х>3, х<-2;
б). (в знаменателе выносим "y" и сокращаем с "y" в числителе)
ответ:
в). (раскрываем числитель по формуле разности квадратов , в знаменателе выносим "3")
ответ:
Задание №2
а). (одинаковый знаменатель, значит можно складывать)
ответ:
б). (знаменатели разные, чтобы сложить приводим к общему знаменателю. Первую дробь умножаем на 4, вторую умножаем на 5, после чего складываем)
ответ:
в). (принцип тот же. "а" есть и там, и там в знаменателе, значит первую дробь умножаем на 3, вторую умножаем на 2, чтобы получить общий знаменатель, после чего вычитаем)
ответ:
г). (знаменатель одинаковый - складываем)
ответ: 2
Задание №3
а). (умножаем первую дробь на a, а вторую умножаем на 2, после чего вычитаем дроби)
ответ:
б). (первую дробь умножаем на знаменатель второй дроби, а вторую дробь умножаем на знаменатель первой дроби, после чего вычитаем)
(ещё можно свернуть по формуле разности квадратов )
ответ:
в). (вынесем "b" в знаменателе второй дроби за скобку и умножим первую дробь на "b", после чего вычитаем)
ответ:
Задание №4
(приведем к общему знаменателю умножив на "2y", после чего сложим)
(теперь подставляем x = -8 и y = 0,1. Десятичное число 0,2 = дроби . Когда получилась трёхэтажная дробь, то знаменатель дроби в знаменателе переносится в числитель и умножается на числитель общей дроби, а знаменатель становится числитель дроби в знаменателе)
ответ: -40
Задание №5
(знаменатель средней дроби раскроем по формуле разности квадратов .
Первую дробь умножим на "х" и на "x+4", среднюю дробь умножим на "х", а третью дробь умножим на "x+4" и на "x-4", после чего посчитаем)
Объяснение: из условий ясно что рядом со всеми липами одинаковые деревья(либо две липы либо две берёзы) и только рядом с одной березой одинаковые деревья. Перебирая все варианты понимаем что условия выполнимы только если сажать деревья так. Л-липа Б- береза. >БЛББЛББЛББЛБББЛББЛББЛБ
Можно заметить в одном три берёзы подряд. Итого если продолжить эту цепочку до 160ти деревьев получим 53 группы БЛБ и одну одинокую березу между БЛБББЛБ . ВСЕ условия выполнены. Рядом с одной березой два одинаковых дерева (две берёзы) а рядом со всеми липами разные деревья (береза и липа).
Задание №1
а).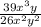 (сокращаем на "13
(сокращаем на "13 y")
y")
ответ: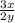
б).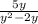 (в знаменателе выносим "y" и сокращаем с "y" в числителе)
(в знаменателе выносим "y" и сокращаем с "y" в числителе)
ответ: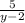
в).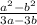 (раскрываем числитель по формуле разности квадратов
(раскрываем числитель по формуле разности квадратов 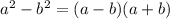 , в знаменателе выносим "3")
, в знаменателе выносим "3")
ответ: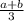
Задание №2
а).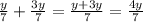 (одинаковый знаменатель, значит можно складывать)
(одинаковый знаменатель, значит можно складывать)
ответ: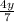
б).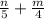 (знаменатели разные, чтобы сложить приводим к общему знаменателю. Первую дробь умножаем на 4, вторую умножаем на 5, после чего складываем)
(знаменатели разные, чтобы сложить приводим к общему знаменателю. Первую дробь умножаем на 4, вторую умножаем на 5, после чего складываем)
ответ: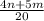
в). (принцип тот же. "а" есть и там, и там в знаменателе, значит первую дробь умножаем на 3, вторую умножаем на 2, чтобы получить общий знаменатель, после чего вычитаем)
(принцип тот же. "а" есть и там, и там в знаменателе, значит первую дробь умножаем на 3, вторую умножаем на 2, чтобы получить общий знаменатель, после чего вычитаем)
ответ: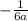
г).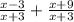 (знаменатель одинаковый - складываем)
(знаменатель одинаковый - складываем)
ответ: 2
Задание №3
а).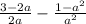 (умножаем первую дробь на a, а вторую умножаем на 2, после чего вычитаем дроби)
(умножаем первую дробь на a, а вторую умножаем на 2, после чего вычитаем дроби)
ответ: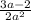
б). (первую дробь умножаем на знаменатель второй дроби, а вторую дробь умножаем на знаменатель первой дроби, после чего вычитаем)
(первую дробь умножаем на знаменатель второй дроби, а вторую дробь умножаем на знаменатель первой дроби, после чего вычитаем)
ответ: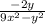
в).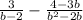 (вынесем "b" в знаменателе второй дроби за скобку и умножим первую дробь на "b", после чего вычитаем)
(вынесем "b" в знаменателе второй дроби за скобку и умножим первую дробь на "b", после чего вычитаем)
ответ: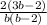
Задание №4
ответ: -40
Задание №5
Первую дробь умножим на "х" и на "x+4", среднюю дробь умножим на "х", а третью дробь умножим на "x+4" и на "x-4", после чего посчитаем)
ответ:53 липы 107 берез.
Объяснение: из условий ясно что рядом со всеми липами одинаковые деревья(либо две липы либо две берёзы) и только рядом с одной березой одинаковые деревья. Перебирая все варианты понимаем что условия выполнимы только если сажать деревья так. Л-липа Б- береза. >БЛББЛББЛББЛБББЛББЛББЛБ
Можно заметить в одном три берёзы подряд. Итого если продолжить эту цепочку до 160ти деревьев получим 53 группы БЛБ и одну одинокую березу между БЛБББЛБ . ВСЕ условия выполнены. Рядом с одной березой два одинаковых дерева (две берёзы) а рядом со всеми липами разные деревья (береза и липа).