Используем формулу косинуса тройного угла и выносим затем общий множитель за скобки:
Замечаем, что второй множитель всегда положителен, поскольку имеет вид суммы квадрата, который всегда неотрицателен, и единицы, прибавление которой делает все выражение только положительным. Первый же множитель уже может быть как положительным, так и отрицательным. Стало быть, для положительности всего произведения он должен быть только положительным. Значит, неравенство равносильно следующему:
Это неравенство уже вполне известно, как решать. Сначала ради удобства сделаем замену .
Ну и дальше это простейшее неравенство решаем с окружности.
Полагаю, что вы опечатались, и функция имеет вид: Для того, чтобы решить задачу, нужно найти координаты вершины по формуле: , где b = +6, a = -1. Так как коэффициент при х отрицательный, то функция возрастает на промежутке от минус бесконечности до значения х вершины, и убывает отсюда до + беск. Область значения функции меняется от минус беск. ветви вниз) до у вершины. Вам осталось только подставить в формулу числа, найти сначала х вершины, потом у вершины. А для построения графика удобно брать точки, равноудалённые от вершины. Удачи!
Объяснение:
Используем формулу косинуса тройного угла и выносим затем общий множитель за скобки:
Замечаем, что второй множитель всегда положителен, поскольку имеет вид суммы квадрата, который всегда неотрицателен, и единицы, прибавление которой делает все выражение только положительным. Первый же множитель уже может быть как положительным, так и отрицательным. Стало быть, для положительности всего произведения он должен быть только положительным. Значит, неравенство равносильно следующему:
Это неравенство уже вполне известно, как решать. Сначала ради удобства сделаем замену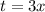 .
.
Ну и дальше это простейшее неравенство решаем с окружности.
Относительно t решение:
Относительно x:
Для того, чтобы решить задачу, нужно найти координаты вершины по формуле: