Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например, , но сейчас это не нужно), нам повезло, это 32
Учитываем, что , получаем
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
Остаток 21, чудесно. Выполняем последний шаг.
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
Если хотя бы одна цифра в записи 0,то произведение равно 0,а сумма равна 1,единственное такое число -1000,но оно не кратно 13. Следовательно нулей среди цифр нет ,значит все цифры не меньше 1,их сумма не меньше 4,а значит произведение цифр не меньше 3 Чтобы произведение не было меньше 3,хотя бы одна из цифр должна быть больше 1, рассмотрим числа в порядке возрастания из суммы Если сумма 5,то число записывается одной 2 и тремя 1(это 1112,1121,1211,2111) произведение цифр рвано 2,следовательно они не удовлетворяют условию Если сумма 6,записывается как одна 3 и тремя 1 ИЛИ двумя 2 и двумя 1(1113,1131,1311,3111,1122,1212,)произведения этих чисел равно 3 или 4 соответственно ,следовательно идём дальше Если сумма 7,то произведение должно 6,эти числа записываются двойкой ,тройкой и двумя единицами (2113,2131,2311,3211) число 3211 кратно 13, оно и подходит P.s расписывал не для лайков и ,не путайся в будущем ,удачи :)
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например,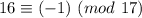 , но сейчас это не нужно), нам повезло, это 32
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что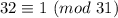 , получаем
, получаем
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
Остаток 21, чудесно. Выполняем последний шаг.
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
Чтобы произведение не было меньше 3,хотя бы одна из цифр должна быть больше 1, рассмотрим числа в порядке возрастания из суммы
Если сумма 5,то число записывается одной 2 и тремя 1(это 1112,1121,1211,2111) произведение цифр рвано 2,следовательно они не удовлетворяют условию
Если сумма 6,записывается как одна 3 и тремя 1 ИЛИ двумя 2 и двумя 1(1113,1131,1311,3111,1122,1212,)произведения этих чисел равно 3 или 4 соответственно ,следовательно идём дальше
Если сумма 7,то произведение должно 6,эти числа записываются двойкой ,тройкой и двумя единицами (2113,2131,2311,3211) число 3211 кратно 13, оно и подходит
P.s расписывал не для лайков и ,не путайся в будущем ,удачи :)