Объяснение:
Эта задача имеет два принципиально разных решения.
А) считаем, что все голубые шары одинаковы между собой, и все розовые тоже одинаковы.
Тогда:
1) двумя : вынуть розовый шар или вынуть голубой шар.
2) тоже двумя : сначала вынуть розовый шар, потом голубой, или наоборот, сначала голубой шар, а потом розовый.
Б) считаем, что все шары разные, например, имеют номера, как в бильярде.
.
Допустим, мы первым вынимаем голубой шар. Это 6 разных .
За ним вынимаем розовый, это 8 разных .
Всего вынуть сначала голубой шар, потом розовый.
И ещё вынуть, наоборот, сначала розовый шар, потом голубой.
Уравнение вида называется квадратным уравнением.
а) Если один из коэффициентов или с равен нулю, то уравнение называется неполным . Данное уравнение неполное квадратное уравнение.
б) старший коэффициент а= 4;
второй коэффициент b= 16;
свободный член с= 0
в) решим данное уравнение. Для этого вынесем 4х ха скобки и разложим левую часть уравнения на множители.
Произведение равно нулю, если хотя бы один из множителей равен нулю, а другой при этом определен
х=0 или х+4=0
х= - 4
Данное уравнение имеет два корня - 4 и 0 .
Объяснение:
Эта задача имеет два принципиально разных решения.
А) считаем, что все голубые шары одинаковы между собой, и все розовые тоже одинаковы.
Тогда:
1) двумя : вынуть розовый шар или вынуть голубой шар.
2) тоже двумя : сначала вынуть розовый шар, потом голубой, или наоборот, сначала голубой шар, а потом розовый.
Б) считаем, что все шары разные, например, имеют номера, как в бильярде.
Тогда:
.
Допустим, мы первым вынимаем голубой шар. Это 6 разных .
За ним вынимаем розовый, это 8 разных .
Всего вынуть сначала голубой шар, потом розовый.
И ещё вынуть, наоборот, сначала розовый шар, потом голубой.
Объяснение:
Уравнение вида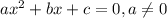
называется квадратным уравнением.
а) Если один из коэффициентов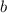
или с равен нулю, то уравнение называется неполным . Данное уравнение неполное квадратное уравнение.
б) старший коэффициент а= 4;
второй коэффициент b= 16;
свободный член с= 0
в) решим данное уравнение. Для этого вынесем 4х ха скобки и разложим левую часть уравнения на множители.
Произведение равно нулю, если хотя бы один из множителей равен нулю, а другой при этом определен
х=0 или х+4=0
х= - 4
Данное уравнение имеет два корня - 4 и 0 .