Огромная решить и прикрепить полное решение и ответы. Буду очень благодарна. Очень

Показать ответ

Ответ:

miwe10

05.08.2020 04:48

Трактовка задач:
1) так как нам дана функция, s(t) это значит что это некое расстояние. Если от этого «расстояния» взять производную, то получим скорость роста.
Берём производную, и после его в t подставляем 4. И находим скорость. Она будет 60м/с. Метры, потому что функция задана с S, в условии это метры.
2) так как k=f'(х₀)=tgα
А x₀=1 то найдём производную функции,
И подставим в производную этот икс нулевой. Получаем -2 tg a=-2
Отсюда находим а.
Последнее задание немного у меня не взлезло, извините
плс , Алгебра. Если можно, оветы с решениями и обьяснениями.

плс , Алгебра. Если можно, оветы с решениями и обьяснениями.

0,0(0 оценок)

Ответ:

briliant2

04.01.2020 15:08

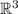Пусть $\varepsilon$ - канонический базис в $\mathbb{R}^{3}$ .

Тогда матрицу перехода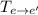 $T_{e \rightarrow e'}$ можно найти следующим образом:

$T_{e \rightarrow e'} = T_{e \rightarrow \varepsilon} \cdot T_{\varepsilon \rightarrow e'} = T_{\varepsilon \rightarrow e}^{-1} \cdot T_{\varepsilon \rightarrow e'}$

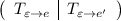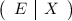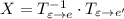
Если записать блочную матрицу $\left(\begin{array}{c|c}T_{\varepsilon \rightarrow e}&T_{\varepsilon \rightarrow e'}\end{array}\right)$ и привести путем элементарных преобразований к виду $\left(\begin{array}{c|c}E&X\end{array}\right)$ , то $X = T_{\varepsilon \rightarrow e}^{-1} \cdot T_{\varepsilon \rightarrow e'}$

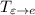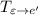Матрицу $T_{\varepsilon \rightarrow e}$ легко получить: достаточно записать в столбцы координаты векторов базиса . Аналогично с матрицей $T_{\varepsilon \rightarrow e'}$ .

В итоге необходимо получить вид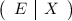 $\left(\begin{array}{c|c}E&X\end{array}\right)$ следующей матрицы:

$\left(\begin{array}{ccc|ccc}2&-1&1&5&7&1\\2&2&-1&5&8&1\\3&-3&2&-1&9&2\end{array}\right)$

Вычтем первую строку из второй и третьей:

$\left(\begin{array}{ccc|ccc}2&-1&1&5&7&1\\0&3&-2&0&1&0\\1&-2&1&-6&2&1\end{array}\right)$

Вычтем из первой строки 2 третьих и поменяем их местами:

$\left(\begin{array}{ccc|ccc}1&-2&1&-6&2&1\\0&3&-2&0&1&0\\0&3&-1&17&3&-1\end{array}\right)$

Вычтем из третьей строки вторую:

$\left(\begin{array}{ccc|ccc}1&-2&1&-6&2&1\\0&3&-2&0&1&0\\0&0&1&17&2&-1\end{array}\right)$

Прибавим ко второй строке 2 третьих и вычтем из первой третью:

$\left(\begin{array}{ccc|ccc}1&-2&0&-23&0&2\\0&3&0&34&5&-2\\0&0&1&17&2&-1\end{array}\right)$

Делим вторую строку на 3:

$\left(\begin{array}{ccc|ccc}1&-2&0&-23&0&2\\0&1&0&\frac{34}{3} &\frac{5}{3}&{-\frac{2}{3}}\\0&0&1&17&2&-1\end{array}\right)$

Прибавляем в первой строке 2 вторых:

$\left(\begin{array}{ccc|ccc}1&0&0&{-\frac{1}{3}}&\frac{10}{3}&\frac{2}{3}\\0&1&0&\frac{34}{3} &\frac{5}{3}&{-\frac{2}{3}}\\0&0&1&17&2&-1\end{array}\right)$