Решим уравнение в зависимости от значений параметра (постоянной)
Применим классическое решение уравнения типа
1) Найдем те значения , при которых обнуляются модули - это и
2) Выставим на координатной оси эти значения:
3.1) Рассмотрим промежуток :
Выясним значение выражений подмодульных выражений:
Раскроем данные модули. Если подмодульное выражение меньше нуля, то для того чтобы его раскрыть, нужно изменить знак выражение, тем самым модуль раскроется с неотрицательным выражением.
Если , то , что верно при любых из рассматриваемого промежутка
Если , то
3.2. Рассмотрим промежуток :
Выясним значение выражений подмодульных выражений:
Раскроем данные модули:
Если , то , что верно при любых из рассматриваемого промежутка
Если , то
Однако, 3 не входит в данный интервал, который мы рассматриваем.
3.3. Рассмотрим промежуток :
Выясним значение выражений подмодульных выражений:
Раскроем данные модули:
Если , то , что неверно ни при каких
Если , то
Рассмотрим данный ответ на заданном интервале. Этот ответ нам подойдет, если выполниться условие:
Решим уравнение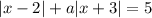 в зависимости от значений параметра (постоянной)
в зависимости от значений параметра (постоянной) 
Применим классическое решение уравнения типа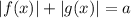
1) Найдем те значения , при которых обнуляются модули - это
, при которых обнуляются модули - это 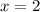 и
и 
2) Выставим на координатной оси эти значения:
эти значения:
3.1) Рассмотрим промежуток![x \in (-\infty; -3]](/tpl/images/1025/4528/6d9ac.png) :
:
Выясним значение выражений подмодульных выражений:
Раскроем данные модули. Если подмодульное выражение меньше нуля, то для того чтобы его раскрыть, нужно изменить знак выражение, тем самым модуль раскроется с неотрицательным выражением.
Если , то
, то  , что верно при любых
, что верно при любых  из рассматриваемого промежутка
из рассматриваемого промежутка
Если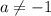 , то
, то 
3.2. Рассмотрим промежуток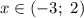 :
:
Выясним значение выражений подмодульных выражений:
Раскроем данные модули:
Если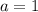 , то
, то  , что верно при любых
, что верно при любых  из рассматриваемого промежутка
из рассматриваемого промежутка
Если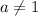 , то
, то 
Однако, 3 не входит в данный интервал, который мы рассматриваем.
3.3. Рассмотрим промежуток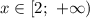 :
:
Выясним значение выражений подмодульных выражений:
Раскроем данные модули:
Если , то
, то 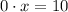 , что неверно ни при каких
, что неверно ни при каких 
Если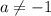 , то
, то 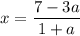
Рассмотрим данный ответ на заданном интервале. Этот ответ нам подойдет, если выполниться условие:
Решим данное неравенство методом интервалов:
1)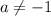
2)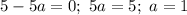
Отметим данные точки на координатной оси
Таким образом,![a \in (-1; \ 1]](/tpl/images/1025/4528/68d76.png)
ЕслиПереписывать не буду выражение сразу буду считать.
а) 1.42/25*15/7 (сокращаем) =6/5*3=18/5=3.6
2.18/7*7/5 (сокращаем) =18*0.2=3.6
3.3.6-3.6=0
4.0*2 7/9=0
Б) 1. 19/8-11/6(нок 24)=57-44/24=13/24
2.1/13*13/24 (сокращаем) =1/24
3.1/24*12/5 (сокращаем) =0.5*0.2=0.1
4.0.1+0.9=1
В)1.7/5*5/2 (сокращаем) =7*0.5=3.5
2.19/4-3.5=4.75-3.5=1. 25
3.1.25*8/5=1.25*1.6=2
Г)1. 36-784/25=900-784/25=116/25
2. 3/2*2/9 (Сокращаем) =1/3
3.1/3-116/25(нок 75)=25-348/75=-4.307
(вроде так, но не уверенна)
Д)1. 61/15-39/10(нок 30)=122-117/30=5/30=1/6
2.1/6*48/7(сокращаем) =8/7
3.8/7+2(нок 7)=8+14/7=22/7=3.14
(вроде так)
Е) 1.4-27/8=5/8
2.3-37/15=8/15
3.5/8*8/15=1/3
4.1/3*1/3=1/9