За 1 час или 60 минут минутная стрелка совершает полный оборот по циферблату,т.е. оборот на 360°. Пройденный угол минутной стрелки: т.е. каждая пройденная минута смещает минутную стрелку на 6°
Пройденный угол часовой стрелки: т.е. каждый пройденный час смещает часовую стрелку на 30°
По условию время 5ч 40 мин, значит угол, пройденный часовой стрелкой угол, пройденный минутной стрелкой Тогда угол между стрелками равен:
ответ: 70°
или
За 1 час или 60 минут минутная стрелка совершает полный оборот по циферблату,т.е. оборот на 360°. смещение часовой стрелки за каждый час смещение часовой стрелки за каждую минуту смещение минутной стрелки за каждую минуту такой угол в градусах опишет часовая стрелка такой угол в градусах опишет минутная стрелка угол между стрелками
В условие задачи дано, что тела начали двигаться из одной и той же точки, поэтому их пути дол встречи будут равны. Найдём уравнение пути каждого из тел
За 1 час или 60 минут минутная стрелка совершает полный оборот по циферблату,т.е. оборот на 360°.
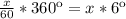
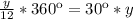
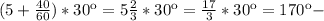 угол, пройденный часовой стрелкой
угол, пройденный часовой стрелкой
 угол, пройденный минутной стрелкой
угол, пройденный минутной стрелкой
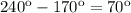
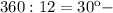 смещение часовой стрелки за каждый час
смещение часовой стрелки за каждый час
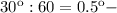 смещение часовой стрелки за каждую минуту
смещение часовой стрелки за каждую минуту
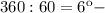 смещение минутной стрелки за каждую минуту
смещение минутной стрелки за каждую минуту
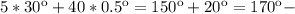 такой угол в градусах опишет часовая стрелка
такой угол в градусах опишет часовая стрелка
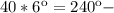 такой угол в градусах опишет минутная стрелка
такой угол в градусах опишет минутная стрелка
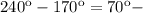 угол между стрелками
угол между стрелками
Пройденный угол минутной стрелки:
т.е. каждая пройденная минута смещает минутную стрелку на 6°
Пройденный угол часовой стрелки:
т.е. каждый пройденный час смещает часовую стрелку на 30°
По условию время 5ч 40 мин, значит
Тогда угол между стрелками равен:
ответ: 70°
или
За 1 час или 60 минут минутная стрелка совершает полный оборот по циферблату,т.е. оборот на 360°.
ответ: 70°
В условие задачи дано, что тела начали двигаться из одной и той же точки, поэтому их пути дол встречи будут равны. Найдём уравнение пути каждого из тел
S1 = ∫ (3t^2 + 4t) dt = t^3 + 2t^2S2 = ∫ (6t + 12) dt = 3t^2 + 12t
Постоянные интегрирования без начальных условиях:
t = 0, S = 0, будут равны нулю.
Встреча этих тел произойдёт при S1 = S2, откуда
t^3 + 2t^2 = 3t^2 + 12t или
t^3 - t^2 - 12t = 0
Решим это уравнение
t (t^2 - t - 12) = 0
t (t - 4)(t + 3) = 0
t = 0, t = 4, t = - 3
В момент t = 4c произойдёт встреча этих тел после начала движения.
Из уравнений пути находим
S1 = S2 = 4^3 + 2*4^2 = 96 м