Перейди от математической модели к словесной.
{15x+7y=1535y−3=7x
Помагите коров и 7 лошадей ежедневно вместе получали 153 кг сена.
Сколько сена ежедневно скармливали каждой корове и каждой лошади, если 5 лошадей получали сена на 3 кг , чем 7 коров?

(В первое окошко введи число, а не слово.)

Из 12 учеников, выбрать ученика, которому мы дадим первую книгу, можно После этого остается 11 учеников без книг. Из них выбрать следующего ученика, которому мы дадим вторую книгу, можно

Общее число раздать разные (!) книги существует .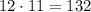

Другими словами, мы находили размещение из 12 по 2:

А вот если книги были бы одинаковыми, то порядок выбора учеников был бы не важен: все выбранные ученики получили бы одинаковые книги. В этом случае мы вычисляем сочетание из 12 по 2:

Итак, если учитель раздает разные книги, то существует это сделать. А соответствует случаю, если раздаваемые книги одинаковые.

ответ: 132

1)

(1-2х)/(2х+1)+(х²+3х)/((2х-1)*(2х+1))+(3+х)/(2(2х+1))=

(-2*(4х²-4х+1)+2х²+6х+6х-3+2х²-х)/(2*(4х²-1))=

(-8х²+8х-2+4х²+12х-х-3)/(2*(4х²-1))=(-4х²+19х-5)/(2*(4х²-1))

Вместо плюса, скорее всего, где-то минус, может опечатка, но ответ верный.

2)

1)((6а+1)*(а+3)+(6а-1)*(а-3))/((а+3)*(а-3))=

(6а²+18а+а+3+6а²-18а-а+3)/((а+3)*(а-3))=6(2а²+1)/((а+3)*(а-3));

2) (а²-9)*6*(2а²+1)/(а²-9)*(2а²+1)=6

3)

1)((а-b)*b/(a*(a-c)))*((a-c)*(a+c)/((a-b)(a+b))=((а-b)*b(a-c)*(a+c)/((a*(a-c))(a-b)(a+b))=(ab+bc)/(a*(a+b))

(b-c)/(a+b)-(ab+bc)/(a*(a+b))=(ab-ac-ab-bc)/(a*(a+b))=-c*(a+b)/(a*(a+b))=-c/a