Площадь прямоугольного участка земли равна ( x2 -19x+88) м2 а) х2 -19x +88=( x + a)(x +b) Найдите a и b. в) Пусть (x + a) м - длина участка, а (x + b) м - его ширина. Запишите, чему равен периметр участка, используя полученные значения a и b.
A) Верно, так как это теорема о задание арифметической прогрессии формулой an = kn + b, где k, b - некоторые числа.
Теорема. Любая арифметическая прогрессия (аn) может быть задана формулой an = kn + b, где k и b - некоторые числа; также имеет место обратное утверждение, если последовательность (аn) задана формулой an = kn + b, где k и b - некоторые числа, то эта последовательность является арифметической прогрессией.
Б) Не верно. Верна формула
В) Неверно. Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних:
Чтобы число было больше в три раз больше наибольшого делителя то все простые множители этого делителя долдны быть больше трех чтобы он был наибольшим. Если одним из простых множителей будет два то будет делитей который вместо этой двойки будет содержать тройку. Следует делитель не будет наибольшим.
Из наших рассуждений следует что наименьший делитель после 1 это 3. Какой-то делитель в десять раз меньше самого числа, но это невозможно так как делителем 10 равняется 2 следует наименьшим делителем будет 2, а не 3, противоречие!
A) Верно, так как это теорема о задание арифметической прогрессии формулой an = kn + b, где k, b - некоторые числа.
Теорема. Любая арифметическая прогрессия (аn) может быть задана формулой an = kn + b, где k и b - некоторые числа; также имеет место обратное утверждение, если последовательность (аn) задана формулой an = kn + b, где k и b - некоторые числа, то эта последовательность является арифметической прогрессией.
Б) Не верно. Верна формула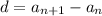
В) Неверно. Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних:
Чтобы число было больше в три раз больше наибольшого делителя то все простые множители этого делителя долдны быть больше трех чтобы он был наибольшим. Если одним из простых множителей будет два то будет делитей который вместо этой двойки будет содержать тройку. Следует делитель не будет наибольшим.
Из наших рассуждений следует что наименьший делитель после 1 это 3. Какой-то делитель в десять раз меньше самого числа, но это невозможно так как делителем 10 равняется 2 следует наименьшим делителем будет 2, а не 3, противоречие!