если 2 множества не равны, то в 1 множестве есть элемент который больше других элементов другого множества. Покажем, что нам выгодно увеличивать 1 элемент множества, чтобы увеличить его сумму в степени n: докажем это.
скажем что a > b
(a ^ n) + b ^ n < (a + 1) ^ n + (b - 1) ^ n
это можно увидеть раскрыв скобки и приведя подобные
следовательно если 2 множества различны или не равны 0 система не выполняется
Пусть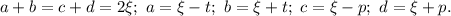
Пусть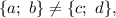
тогда t≠±p; не уменьшая общности, можно считать, что 
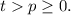Пусть n=2k+1. Используя бином Ньютона, можем написать
Это выражение может равняться нулю только если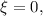
а это и означает, что a=-b; c=-d. Утверждение доказано.
если 2 множества не равны, то в 1 множестве есть элемент который больше других элементов другого множества. Покажем, что нам выгодно увеличивать 1 элемент множества, чтобы увеличить его сумму в степени n: докажем это.
скажем что a > b
(a ^ n) + b ^ n < (a + 1) ^ n + (b - 1) ^ n
это можно увидеть раскрыв скобки и приведя подобные
следовательно если 2 множества различны или не равны 0 система не выполняется