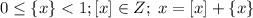Алгебра: Представь в виде произведения: a2 + a – b2 – b

Представь в виде произведения: a2 + a – b2 – b

Показать ответ

Ответ:

nastyagrigorov

23.11.2022 05:03

Высоты треугольника пересекаются в одной точке.

Следовательно, достаточно найти уравнения двух любых высот треугольника и точку их пересечения, решив систему двух уравнений.

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Значит надо найти уравнение стороны треугольника и уравнение прямой, проходящей через противоположную вершину, перпендикулярно этой стороне.

Уравнение прямой АВ найдем по формуле:

(X-Xa)/(Xb-Xa)=(Y-Ya)/(Yb-Ya). Или

(X+4)/2=(Y-0)/-2 - каноническое уравнение =>

y=-x-2 - уравнение прямой с угловым коэффициентом k=-1.

Условие перпендикулярности прямых: k1=-1/k => k1=1.

Тогда уравнение перпендикуляра к стороне АВ из вершины С

найдем по формуле:

Y-Yс=k1(X-Xс) или Y-2=X-2 =>

y=х (1) - это уравнение перпендикуляра СС1.

Уравнение прямой АС:

(X-Xa)/(Xс-Xa)=(Y-Ya)/(Yс-Yа). Или

(X+4)/6=(Y-0)/2 - каноническое уравнение =>

y=(1/3)x+4/3 - уравнение прямой с угловым коэффициентом k=1/3.

Условие перпендикулярности прямых: k1=-1/k => k1 = -3.

Тогда уравнение перпендикуляра к стороне АС из вершины В

найдем по формуле:

Y-Yb=k1(X-Xb) или Y+2=-3(X+2) =>

y=-3х-8 (2)- это уравнение перпендикуляра BB1.

Точка пересечения перпендикуляров имеет координаты:

х=-3х - 8 (подставили (1) в (2)) => х = -2.

Тогда y = -2.

ответ: точка пересечения высот совпадает с вершиной В(-2;-2)

треугольника, то есть треугольник прямоугольный с <B=90°.

Для проверки найдем длины сторон треугольника:

АВ=√(((-2-(-4))²+(-2)²) = 2√2.

ВС=√(((2-(-2))²+(2-(-2))²) = 4√2.

АС=√(((2-(-4))²+2²) = 2√10.

АВ²+ВС² = 40; АС² = 40.

По Пифагору АВ²+ВС² = АС² - треугольник прямоугольный.

Объяснение:

0,0(0 оценок)

Ответ:

taniussa1

16.04.2023 07:24

По определению,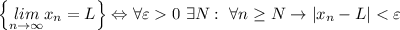 $\left\{\underset{n\rightarrow\infty}{lim}x_n=L\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n-L\right|$

Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение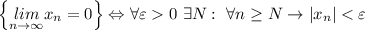 $\left\{\underset{n\rightarrow\infty}{lim}x_n=0\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n\right|$

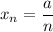
2) $x_n=\dfrac{a}{n}$

|x_n|

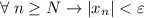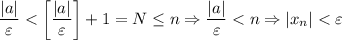
А значит, если взять $N=\left[\dfrac{|a|}{\varepsilon}\right] +1$ (*), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|a|}{\varepsilon}$

(*) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{|a|}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)

А это и означает, что предел данной последовательности равен 0

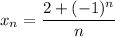
4) $x_n=\dfrac{2+(-1)^n}{n}$

|x_n|

$|2+(-1)^n|=\left\{\begin{array}{c}2-1=1,n=2k-1,k\in N \\2+1=3,n=2k,k\in N \end{array}\right. \Rightarrow |2+(-1)^n|\leq 3\; \forall n\in N$

А значит, если взять $N=\left[\dfrac{3}{\varepsilon}\right] +1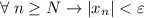$ (**), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|$

(**) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{3}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)

А это и означает, что предел данной последовательности равен 0

___________________________

2) a=1. Тогда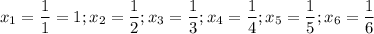 $x_1=\dfrac{1}{1}=1; x_2=\dfrac{1}{2}; x_3=\dfrac{1}{3}; x_4=\dfrac{1}{4}; x_5=\dfrac{1}{5}; x_6=\dfrac{1}{6}$

$x_1=\dfrac{2+(-1)^1}{1}=1;\;x_2=\dfrac{2+(-1)^2}{2}=1\dfrac{1}{2};\;x_3=\dfrac{2+(-1)^3}{3}=\dfrac{1}{3};\;x_4=\dfrac{2+(-1)^4}{4}=\dfrac{3}{4};\;x_5=\dfrac{2+(-1)^5}{5}=\dfrac{1}{5};\;x_6=\dfrac{2+(-1)^6}{6}=\dfrac{1}{2}.$