В точке х₁ = 0 производная меняет знак с - на +, поэтому х₁ = 0 - точка минимума.
В точке х₂ = -5 производная меняет знак с + на -, поэтому х₂ = -5 - точка максимума.
В интервале х ∈ [-6; 1] находятся и точка максимума х₂ = -5 и точка минимума х₁ = 0 , поэтому наибольшее значение функция будет иметь в точке х₂ = -5, а наименьшее значение а точке х₁ = 0
у наиб = у(-5) = 12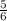
у наим = у(0) = -8
Объяснение:
Функция
Производная функции
y' = x² + 5x
Найдём точки экстремумов
x² + 5x = 0
х(х + 5) = 0
х₁ = 0; х₂ = -5;
В точке х₁ = 0 производная меняет знак с - на +, поэтому х₁ = 0 - точка минимума.
В точке х₂ = -5 производная меняет знак с + на -, поэтому х₂ = -5 - точка максимума.
В интервале х ∈ [-6; 1] находятся и точка максимума х₂ = -5 и точка минимума х₁ = 0 , поэтому наибольшее значение функция будет иметь в точке х₂ = -5, а наименьшее значение а точке х₁ = 0
у наиб = у(-5) = (-5)³/3 + 5 · (-5)²/2 - 8 = -41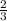
+ 62,5 - 8 = 12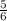
у наим = у(0) = -8
(2√2-√15)\12
Объяснение:
sin(a+b), если соsa=1/3, cosb=1/4, и a€ (0;пи), b € (-пи/2; 0)
sin(α + β) = sinα•cosβ + cosα•sinβ . Нужно найти sinα и sinβ.
1) По основному тригонометрическому тождеству найдем sinα если соsa=1/3 :
sin²а+cos²а=1, sin²а+1\9=1, sin²а=8\9 , sinа=2√2\3 ,т.к. sinа>0 в 1,2 четверти.
2) По основному тригонометрическому тождеству найдем sinb если cosb=1/4 :
sin²b+cos²b=1, sin²b+1\16=1, sin²b=15\16, sinb=-√15\4 ,т.к. sinb<0 в 4 четверти.
Все закидываем в синус суммы :
sin(a+b)=2√2\3 *1\4 +1\3*(-√15\4)=(2√2-√15)\12.