Чтобы для всех x∈[-1;0] неравенство выполнялось, необходимо обеспечить полное вхождение этого отрезка в интервал (-2a; -a-2), то есть:
а) -2a < -1 => a > 0.5
б) 0 < -a-2 => a < -2
Решений для a нет.
2) -2a > -a-2, то есть a < 2
Решением будет x∈(-a-2; -2a).
Чтобы для всех x∈[-1;0] неравенство выполнялось, необходимо обеспечить полное вхождение этого отрезка в интервал (-a-2; -2a), то есть:
а) -a-2 < -1 => a > -1
б) 0 < -2a => a < 0
Получается, что a ∈ (-1; 0)
3) -2a = -a-2, то есть a = 2. Тогда числитель и знаменатель дроби одинаковы, можно разделить их друг на друга и получить 1. Тогда получим неверное неравенство 1 < 0, то есть неравенство не будет иметь вовсе решений.
Таким образом, получается единственный интервал a∈(-1; 0)
a∈(-1; 0)
Объяснение:
Рассмотрим неравенство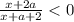 .
.
Рассмотрим 3 случая:
1) -2a < -a-2, то есть a>2
Решением будет x∈(-2a; -a-2).
Чтобы для всех x∈[-1;0] неравенство выполнялось, необходимо обеспечить полное вхождение этого отрезка в интервал (-2a; -a-2), то есть:
а) -2a < -1 => a > 0.5
б) 0 < -a-2 => a < -2
Решений для a нет.
2) -2a > -a-2, то есть a < 2
Решением будет x∈(-a-2; -2a).
Чтобы для всех x∈[-1;0] неравенство выполнялось, необходимо обеспечить полное вхождение этого отрезка в интервал (-a-2; -2a), то есть:
а) -a-2 < -1 => a > -1
б) 0 < -2a => a < 0
Получается, что a ∈ (-1; 0)
3) -2a = -a-2, то есть a = 2. Тогда числитель и знаменатель дроби одинаковы, можно разделить их друг на друга и получить 1. Тогда получим неверное неравенство 1 < 0, то есть неравенство не будет иметь вовсе решений.
Таким образом, получается единственный интервал a∈(-1; 0)