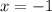запишем для нашего уравнения теорему Виета
x1+x2+x3=3
x1*x2+x2*x3+x1*x3=0
x1*x2*x3=-a
учтем, что по условию один корень уравнеия кратный.
x1+2x2=3
x1*x2^2=-a
x2^2+2x1*x2=0 x2*(x2+2x1)=0
x2=-2x1 подставляем в первое уравнение x1-4x1=-3 -3x1=3 x1=-1 x2=x3=2
X1*X2*X3=-4
т.е. уравнение имеет вид x^3-3x^2+4=0
a=-4
Кубичеcкое уравнение имеет хотя бы два совпадающих корня, когда
(большая, что бы отличать от парметра ),
(по условию )
Проведём проверку:
В глаза бросается очевидный корень уравнения
, если - вида - разаличных корня ровно два.
разаличных корня ровно два.
запишем для нашего уравнения теорему Виета
x1+x2+x3=3
x1*x2+x2*x3+x1*x3=0
x1*x2*x3=-a
учтем, что по условию один корень уравнеия кратный.
x1+2x2=3
x1*x2^2=-a
x2^2+2x1*x2=0 x2*(x2+2x1)=0
x2=-2x1 подставляем в первое уравнение x1-4x1=-3 -3x1=3 x1=-1 x2=x3=2
X1*X2*X3=-4
т.е. уравнение имеет вид x^3-3x^2+4=0
a=-4
Кубичеcкое уравнение имеет хотя бы два совпадающих корня, когда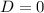
Проведём проверку: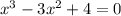
В глаза бросается очевидный корень уравнения