Приведи дроби x^2\x^2-y^2 и x-y\5x+5y к общему знаменателю.

Объяснение:

Пусть они выехали в x час.

Значит, они ехали (16 -x) час. со скоростью v км/час, проехав  расстояние

s = v*(16-x) км.

Если бы скорость была на 25% больше, т.е. 1,25v, то они ехали бы (14,5-x) час., проехав то же расстояние s = 1,25v*(14,5-x).

Приравняем правые части в выражениях для s.

v*(16-x) = 1,25v*(14,5-x)

Решим относительно x, предварительно сократив v.

16-x = 1,25*(14,5-x)

16-x = 18,125 - 1,25x

1,25x -x=18,125-16

0,25x = 2,125

x= 2,125/0,25

x =8,5

ответ: выехали из дома в 8 ч. 30 мин.

Для решения запишем формулу бинома Ньютона:

Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение .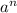

Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение .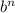

Рассмотрим многочлен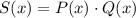 , где:

Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.

Для многочлена :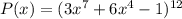

- степень определяется выражением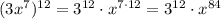 , то есть степень равна 84

- свободный член равен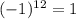

Для многочлена :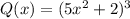

- степень определяется выражением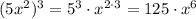 , то есть степень равна 6

- свободный член равен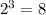

Наконец, для многочлена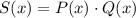 получим:

- степень определяется выражением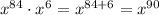 , то есть степень равна 90

- свободный член равен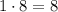

Сумма степени и свободного члена многочлена :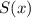

ответ: 98