Пусть x число квартир в подъезде, а однозначный номер стоит s рублей. Поскольку в доме есть трёхзначные номера (они упомянуты) и нет четырёхзначных (они не упомянуты), то число 3x трёхзначно, поэтому x двузначно. Рассмотрим два случая:
1) Пусть число 2x двузначно. Тогда во втором подъезде все номера двузначны, поэтому собрано 2xs руб. В третьем подъезде (99 2x) двузначных номеров и 3x 99 трёхзначных, поэтому в нём собрано 2s(99 2x) + 3s(3x 99) руб. По условию 1,2 2sx = 2s(99 2x) + 3s(3x 99), откуда 2,4x = 5x 99 и x не целое.
2) Пусть число 2x трёхзначно. Тогда во втором подъезде (99 2x) двузначных и (3x 99) трёхзначных номеров, а в третьем x трёхзначных номеров, откуда 1,2(4x 99) = 3x, и x = 66. Проверка показывает, что 2x и 3x действительно трёхзначны.
Пусть x число квартир в подъезде, а однозначный номер стоит s рублей. Поскольку в доме есть трёхзначные номера (они упомянуты) и нет четырёхзначных (они не упомянуты), то число 3x трёхзначно, поэтому x двузначно. Рассмотрим два случая:
1) Пусть число 2x двузначно. Тогда во втором подъезде все номера двузначны, поэтому собрано 2xs руб. В третьем подъезде (99 2x) двузначных номеров и 3x 99 трёхзначных, поэтому в нём собрано 2s(99 2x) + 3s(3x 99) руб. По условию 1,2 2sx = 2s(99 2x) + 3s(3x 99), откуда 2,4x = 5x 99 и x не целое.
2) Пусть число 2x трёхзначно. Тогда во втором подъезде (99 2x) двузначных и (3x 99) трёхзначных номеров, а в третьем x трёхзначных номеров, откуда 1,2(4x 99) = 3x, и x = 66. Проверка показывает, что 2x и 3x действительно трёхзначны.
ответ: 66 квартир.
из условия задачи: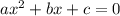
решим систему уравнений, где в одном поменяем a и b, а в другом b и c.
выразим дискриминант в обоих уравнениях и приравняем к 0, т.к. корень должен быть 1.
выразим 4b из первого уравнения и подставим во второе:
т.к.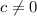
тогда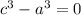
подставим в выражение, где твыразили 4b
подставим все получившиеся коэффициенты в первое уравнеие:
выразим дискриминант:
видно, что дискриминант получится отрицательным, следовательно у данного трехчлена решений нет.
ответ: корней нет