Пусть числитель дроби равен х, тогда знаменатель - (х+1). Если числитель и знаменатель дроби увеличить на 1: , то дробь увеличится на 1/12
Составим уравнение
По теореме Виета
x1 = -5
x2 = 2
5/4 - не соответствует условию.
Исходная дробь: 2/3.
2) Пусть скорость течения реки равна х км/ч, тогда скорость против течения равна (20-x) км/ч, а по течению (20+x) км/ч. Время движения против течения равно 20/(20-x) часов, а по течению - 20/(20+x) часов. На весь путь лодка затратила 2.5 - 25/60= 2.5-5/12 = 25/12 часов.
Пусть числитель дроби равен х, тогда знаменатель - (х+1). Если числитель и знаменатель дроби увеличить на 1: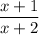 , то дробь увеличится на 1/12
, то дробь увеличится на 1/12
Составим уравнение
По теореме Виета
x1 = -5
x2 = 2
5/4 - не соответствует условию.
Исходная дробь: 2/3.
2) Пусть скорость течения реки равна х км/ч, тогда скорость против течения равна (20-x) км/ч, а по течению (20+x) км/ч. Время движения против течения равно 20/(20-x) часов, а по течению - 20/(20+x) часов. На весь путь лодка затратила 2.5 - 25/60= 2.5-5/12 = 25/12 часов.
Составим уравнение:
Корень х=-4 не удовлетворяет условию.
ответ: скорость течения реки равна 4 км/ч.
1)ОДЗ х2-1 не =0, т.е. (х-1) не =0 и (х+1) не=0, т.е. х не =+-1
Дробь=0, когда числитель=0,т.е. х2-3х+2=0
D=9-8-1, х1=(3+1)/2 х1=2, х2=(3-1)/2 х2=1 этот корень не входит в ОДЗ
ответ: х=2
2) х2-4х+3=0
Д=16-12=4
х1=(4+2)/2 х1=3
х2=(4-2)/2 х2=1
х2+9х=0
х(х+9)=0
х1=0 х2=-9
7х2-х-8=0
Д=1+4*7*8=225
х1=(1+15)/14 х1=1 1/7
х2=(1-15)/14 х2=-1
2х2-50=0
2(х2-25)=0
(х-5)*(х+5)=0
х1=5 х2=-5
3) у2-9у-2=0, ведь это числитель дроби, у которой знаменатель7? Тогда решаем так:
Д=81+8=89
у1=(9+корень из 89)/2
у1=(9-корень из 89)/2