Разделите с остатком многочлен `F(x)` на многочлен `G(x)`. Запишите равенство `F(x)=p(x)*G(x)+r(x)`, где `p(x)` - частное, а `r(x)` - остаток от деления. Проверьте справедливость этого равенства, раскрывая скобки и приводя подобные слагаемые в правой части.

а)(1) `F(x)=x^3+x^2+1`, `G(x)=x^4`;
б)(1) `F(x)=x^5+x-1`, `G(x)=3x^5+x^2-2`;
в)(2) `F(x)=2x^4-3x^3+4x^2-5x+6`, `G(x)=x^2-3x`.

Відповідь:

Пояснення:

Якщо цифри в числі можуть повторюватися, то:

на перше місце числа можна поставити будь-яку цифру з трьох: 2, 3, або вибору;

вибір другої і третьої цифр можна здійснити 4-ма (можна вибрати кожну із даних цифр 0, 2, 3, або 5).

Тоді (за правилом добутку) можна утворити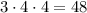 трицифрових чисел.

Якщо цифри в числі не можуть повторюватися, то

на перше місце числа можна поставити будь-яку цифру з трьох: 2, 3, або вибору;

вибір другої цифри можна здійснити теж 3-ма (тут можна поставити і 0);

вибір третьої цифри можна здійснити вже 2-ма .

Тоді (за правилом добутку) можна утворити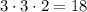 трицифрових чисел.

Пусть в одном пакете было х (икс) кг муки, а в одном пакете у (игрек) кг сахара. Поскольку пакеты с мукой и сахаром были одинаковые, составим первое уравнение: х = у. Муки в 8 пакетах – (х • 8) кг, а сахара в 6 пакетах – (у • 6). Зная разницу в весе (10 кг), составим второе уравнение: х • 8 – у • 6 = 10. Получаем систему уравнений: х = у; х • 8 – у • 6 = 10. Подставим значение икса из первого уравнения во второе:

у • 8 – у • 6 = 10;

у • 2 = 10;

у = 10 : 2;

у = 5 (кг) – в одном пакете сахара;

х = у = 5 (кг) – в одном пакете муки;

Вычислим, сколько весит мука: х • 8 = 5 • 8 = 40 (кг).

Определим, сколько весит сахар: у • 6 = 5 • 6 = 30 (кг)

ответ: мука весит 40 кг, сахар – 30 кг.