Разложить на множители : 1) x^6-1,44= 2) y^12-16= 3) 4x^2y^4-9= 4) 9a^2b^2-64x^4=

ОДЗ: x-2≠0   x+3≠0
         x≠2       x≠-3

4x³+8x²-x-2=0
Решаем уравнение высших степеней.
Находим целые корни: свободный член -2, его делители 1, -1, 2, -2
Подставляем их в исходное равенство до получения тождества.
При х=-2: 4*(-2)³+8*(-2)²-(-2)-2=-32+32+2-2=0
То есть х=-2 является корнем.
Далее разделим многочлен 4x³+8x²-x-2 на (х+2)
4x³+8x²-x-2 |x+2
-                   ------
4x³+8x²        4x²-1
----------
           -x-2
           -x-2
          -------
               0
4x³+8x²-x-2=(x+2)(4x²-1)=(x+2)*(2x-1)(2x+1)
(x+2)(2x-1)(2x+1)=0
x+2=0    2x-1=0     2x+1=0
x=-2       2x=1        2x=-1
              x=1/2       x=-1/2

 №1.

Отметим данные точки и проведём через них прямую.

Прямая пересекает ось Oy в точке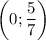 ; ось Ox в точке (1,25;0). Подробнее смотри в приложении.

 №2.

Точка M(x;y):

расположена в 1 четверти, если x>0 и y>0;

расположена во 2 четверти, если x<0 и y>0;

расположена в 3 четверти, если x<0 и y<0;

расположена в 4 четверти, если x>0 и y<0.

Точка A(-87;89) расположена во 2 четверти т.к. -87<0 и 89>0.

Точка B(3,5;2) расположена в 1 четверти т.к. 3,5>0 и 2>0.

Точка C(0,1;-0,001) расположена в 4 четверти т.к. 0,1>0 и -0,001<0.

Точка D(-1,25;-3,48) расположена в 3 четверти т.к. -1,25<0 и -3,48<0.